Piecewise Functions

The event will hold in three days.
Well-cooked and delicious: rice and beans
Fresh avocados
Options of fish, chicken, cabeza
Son: Dad, what about vegan?
Dad: Let's not worry about vegan. Those folks would really be hungry.
They need to eat well.
Son: Does it mean that those who are vegan do not eat well?
Dad: I did not say that. Do not force words into my mouth.
Son: I just asked a question, Dad.
What about al pastor?
Dad: No, we do not eat pork.
Why should we give people what we do not eat?
Okay, let's go and order these burritos.

Dad: Buenas tardes, señora
How are you doing today?
Son: Good afternoon, Mama Esther.
Esther: Good afternoon. I am doing well.
How are you doing too?
Dad: We are doing well.
Thank you.
How much are your burritos?
Esther: It's $7.00 each.
Guacamole costs extra ¢50 each.
Dad: We want to place an order for 1000 burritos.
Son: Well-cooked: rice and beans; fresh avocados...everything
No guacamole.
Esther: Okay...
Dad: 300 pescado; 300 cabeza; 400 chicken
How much is the cost?
Esther: How soon do you need them?
Dad: In three days.
Esther: Would I deliver them, or would you pick them up?
Dad: We shall pick them up.
Esther: It's going to be $7 each for the first 300 burritos
$6 each for the next 300, and $5.00 each for the remaining 400.
Fair enough?
So, the price is ...
$2100 for the first 300 + $1800 for the next 300 + $2000 for the remaining 400
Total of $5900
Add 10% tax of $5900
That gives $590
Total cost of $6490.00

Son: Dad, I could calculate the cost another way.
Dad: What way?
Is it better than the way Esther did?
Son: For many orders, yes!
And for writing a computer program to calculate it.
Dad: Interesting. What is it?
Son: We learned it in school.
Mama Esther did it as a simple Arithmetic.
Mr. C called it the Manual method.
Then, he taught us to do it algebraically ...
using the Piecewise Function method.
I think it is much better.
Dad: Okay, what's the method?
Son: We begin by defining the variables involved.
Let the number of burritos = b
and the cost = c
Which variable depends on the other variable?
Son: Does the number of burritos depend on the cost, or
does the cost depend on the number of burritos?
Dad: The cost depends on the number of burritos.
Son: That is correct.
We write it this way: $c = f(b)$
It can also be written as: $c(b)$
Dad: Okay...
Son: So,

$ c(b) = \begin{cases} 7b; & \quad 1 \leq b \leq 300 \\[3ex] 6b + 300; & \quad 300 \lt b \leq 600 \\[3ex] 5b + 900; & \quad 600 \lt b \leq 1000 \end{cases} $

Dad: How is this better than the way Esther did it?
Son: Say you wanted to order $900$ burritos
How much would it cost excluding the taxes?
Dad: $7 for the first 300 gives $2100
$6 for the next 300 gives $1800
$5 for the remaining 300 gives $1500
That gives a total of $5400
Son: How many steps did you do before you got the answer?
Dad: Three steps...
Son: I shall do only two steps before I get that answer.
$c(900) = 5(900) + 900 = 4500 + 900 = 5400$
Dad: You used the 3rd equation because 900 falls in ...
Son: that piece...yes...in that domain.
Dad: That is interesting! How did you get those equations?
Son: Welcome to Piecewise Functions!, Dad.

Objectives

Students will:
(1.) Define piecewise functions.
(2.) Discuss piecewise functions.
(3.) Discuss real-world applications of piecewise-functions.
(4.) Give examples of mathematical functions that are piecewise functions.
(5.) Graph piecewise functions manually.
(6.) Graph piecewise functions using the Texas Instruments (TI) series graphing calculators.
(7.) Analyze the graphs of piecewise functions.
(8.) Solve problems involving the application of piecewise functions.

Skills Measured/Acquired

(1.) Use of prior knowledge
(2.) Critical Thinking
(3.) Interdisciplinary connections/applications
(4.) Technology
(5.) Active participation through direct questioning
(6.) Project-based learning (PBL) Research.

Homework Assignment

Students should research real-world applications of piecewise functions.

(1.) Write the word problem (real-world application).
(2.) Solve solve questions (numbers) "manually" for each piece/interval.
(3.) Write the piecewise function for the word problem.
(4.) Solve those questions again using the piecewise function.
(5.) Check to ensure that you get the same answers (verify your answers) using both methods (manually and piecewise function).
(6.) Write a computer program that solves that word problem.
(7.) Verify your answers again with the computer program.

Check for prior knowledge. Ask students about these terms.

Vocabulary Words

Bring it to English: piece, step, hybrid, exception, except, condition
Bring it to Math: piecewise, function, piecewise-defined, hybrid, domain, range, intercepts, x-intercept, y-intercept, graph, continuity, discontinuity
Bring it to Computer Science: conditional statements, if, if-else, if-elif

Why Study Piecewise Functions?

Ask students to give examples of scenarios where exceptions have been made, or where certain conditions have been used. Let us begin with a simple example.

At some Golden Corral restaurants in the U.S, children aged 3 years and under (at most 3 years) eat free.
Let us analyze the Kid's Buffet. The information is found here.

                        It is also written here for you: 
                        Ages 3 and under:                   Free 
                        Ages 4 - 8:                         $5.99
                        Ages 9 - 12:                        $6.99 
                    

As you see, there are different prices (costs) for children in a certain age group.
So, you only eat free if you are at most 3 years old. That is a condition that must be satisfied before you eat free.
When writing a computer program for this function, you have to use conditional statements.

Let us write this function as a piecewise function.
First: Define the variables.
Two things are involved in this function: age and cost.
Let $a$ be the age of the child.
Let $c$ be the cost of the meal.
As you can see, the cost of the meal depends on the age of the child.
This means that the cost is the dependent variable.
And the age of the child is the independent variable.
So, the cost of the meal is a function of the age of the child.
$c = f(a)$. We can write this as $c(a)$ pronounced as $c \: of \: a$
$$ c(a) = \begin{cases} \$0 & \quad 0 < a ≤ 3 \\[3ex] \$5.99 & \quad 3 < a ≤ 8 \\[3ex] \$6.99 & \quad 8 < a ≤ 12 \end{cases} $$

Exercises

Use the piecewise function above and answer these questions.

(1.) Peter is 3 years old.
How much (excluding taxes) is the cost of his meal?

Show/Hide Answer

(2.) Mary is 7 years old.
How much (including taxes) is the cost of her meal?
Assume Golden Corral charges a tax rate of 7.5%.

Show/Hide Answer

Students should give more examples as seen in national parks, car rentals, and retail stores among others.
They should cite their sources "properly".
Teachers should emphasize the importance of citing sources accurately, and citing them in the correct format.

What is a Piecewise Function?

A piecewise function is a function consisting of sub-functions (pieces) defined on a sequence of intervals (domains).
It is also known as a piecewise-defined function or hybrid function.
It is function defined by different equations/functions on different parts of its​ domain.
The domain of each function must not overlap.

Ask students why the domains must not overlap. What would happen if the domains of any two sub-functions overlap?
Some students may ask you that question first. If they do, ask them for their opinions.

As of the 30th day of December, 2018; the power rates for the Residential Service during the Summer Period (June - September) by Georgia Power is found here.

We shall focus on the Residential Service Rates. These costs exclude taxes and other costs.

                    It is also written here for you: 

                    Basic Service:                $10.00   

                    First 650KWh:                 ¢5.7 per KWh  

                    650 - 1000KWh:                ¢9.4 per KWh  

                    Over 1000KWh:                 ¢9.7 per KWh 
                    

KWh means kilowatt hour.
$1$ KWh = $3600000$ J
$1$ kilowatt hour is equivalent to $3600000$ Joules.
The S.I (System International) unit of power is the Joule, $J$
The basic service fee is in dollars.
The rate of consumption is in cents.
We have to convert to the same unit.
We shall use the dollars (not the cents).
$ \$1 = ¢100 \\[2ex] ¢100 = \$1 \\[2ex] ¢5.7 = \$0.057 \\[2ex] ¢9.4 = \$0.094 \\[2ex] ¢9.7 = \$0.097 $

But, please wait a minute!

That information is not "really" correct.
The "Interactive Sample Bill" (hmmmm....it is not interactive though ☺☺☺) found here is also incorrect.

The correct information is found in the Georgia Power Bill Calculator of the Georgia Public Service Commission.
The correct information is here
It is great to know that the Georgia Public Service Commission developed a Power Bill calculator.
We shall check our work with their calculator.
And of course...we shall also check our work with my calculator.

                    The correct information is written here for you: 

                    Basic Service:          $10.00   

                    Tier                    Usage                   Cost per KWh 

                    1st tier                up to 650KWh            $0.056582 

                    2nd tier                next 350KWh             $0.093983 

                    3rd tier                over 1000KWh            $0.097273 
                    

Teaching Moments (to promote critical thinking)
Ask students to explain the differences between the information found in the Georgia Power website (the first one) and that found in the Georgia Public Service Commission (the second one).
Students should also explain the differences based on the domains of each piece in both websites.
What are the errors in the first one?
Please specify the importance of not rounding intermediate calculations.
Please specify the importance of rounding only the final answer to two decimal place (because it is dollars and cents).

---

Calculate the power costs for the following consumption of power.

(1.) $0$ KWh
(2.) $300$ KWh
(3.) $700$ KWh
(4.) $1000$ KWh
(5.) $1200$ KWh

Solution: $1st$ Method: Manual/Arithmetic Method

This application has three pieces.
The basic service fee is not a piece. It must be paid whether one consumed any power or not.
Let $p$ = power (in KWh)
Let $r$ = cost (in dollars per KWh)
(1.) $0$ KWh falls in the first piece.
Basic service fee = $$10.00$
cost for $0$ KWh @ $$0.056582$ per KWh = $0 * 0.056582 = 0$
$10.00 + 0.00 = 10.00$
cost for $0$ KWh = $$10.00$

(2.) $300$ KWh falls in the first piece.
Basic service fee = $$10.00$
cost for $300$ KWh @ $$0.056582$ per KWh = $300 * 0.056582 = 16.9746$
$10.00 + 16.9746 = 26.9746$
cost for $300$ KWh = $$26.97$

(3.) $700$ KWh falls in the second piece.
Basic service fee = $$10.00$
Before we use the second piece, we have to go through the first piece first.
First Piece for $650$ KWh
cost for $650$ KWh @ $$0.056582$ per KWh = $650 * 0.056582 = 36.7783$
$700 - 650 = 50$
We need to find the cost for the remaining $50$ KWh
That takes us to the second piece.
Second Piece for $50$ KWh
cost for $50$ KWh @ $$0.093983$ per KWh = $50 * 0.093983 = 4.69915$
$10.00 + 36.7783 + 4.69915 = 51.47745$
cost for $700$ KWh = $$51.48$

(4.) $1000$ KWh falls in the second piece.
Basic service fee = $$10.00$
Before we use the second piece, we have to go through the first piece first.
First Piece for $650$ KWh
cost for $650$ KWh @ $$0.056582$ per KWh = $650 * 0.056582 = 36.7783$
$1000 - 650 = 350$
We need to find the cost for the remaining $350$ KWh
That takes us to the second piece.
Second Piece for $350$ KWh
cost for $350$ KWh @ $$0.093983$ per KWh = $350 * 0.093983 = 32.89405$
$10.00 + 36.7783 + 32.89405 = 79.67235$
cost for $1000$ KWh = $$79.67$

(5.) $1200$ KWh falls in the third piece.
Basic service fee = $$10.00$
Before we use the third piece, we have to go through the first piece and also through the second piece.
First Piece for $650$ KWh
cost for $650$ KWh @ $$0.056582$ per KWh = $650 * 0.056582 = 36.7783$
$1000 - 650 = 350$
We need to find the cost for $350$ KWh
That takes us to the second piece.
Second Piece for $350$ KWh
cost for $350$ KWh @ $$0.093983$ per KWh = $350 * 0.093983 = 32.89405$
$1200 - 1000 = 200$
We need to find the cost for the remaining $200$ KWh
That takes us to the third piece.
Third Piece for $200$ KWh
cost for $200$ KWh @ $$0.097273$ per KWh = $200 * 0.097273 = 19.4546$
$10.00 + 36.7783 + 32.89405 + 19.4546 = 99.12695$
cost for $1200$ KWh = $$99.13$

Some students may ask if it is possible to have just one function that will find the cost for any consumption of power.
Or is it possible to find the cost for the consumption of power that falls in the second piece, without having to go through the first piece?
Those are really interesting questions!
That is one of the reasons for studying piecewise functions ☺☺☺

Please specify the importance of not rounding intermediate calculations.
Please specify the importance of rounding only the final answer to two decimal place (because it is dollars and cents).

Solution: $2nd$ Method: Piecewise Function/Algebraic Method

What if we have to calculate the power rates for "several" consumption of power?
Do we have to solve this manually all the time? That will be time consuming!
We can write it as a piecewise function and use each function for the consumption of power that correspond to that piece.
Besides, writing it as a piecewise function helps us to write a computer program that will find the rate for any consumption of power.
This application has three pieces.
Let $p$ = power consumed(in KWh)
Let $c$ = cost per KWh or power consumed (in dollars)
$c = f(p)$
This can be written as: $c(p)$

For the first piece;
Basic service fee = $$10.00$
cost for $p$ KWh @ $$0.056582$ per KWh = $p * 0.056582 = 0.056582p$
$10 + 0.056582p = 0.056582p + 10$
$c(p) = 0.056582p + 10$

For the second piece;
Basic service fee = $$10.00$
We have to "finish" with the first piece first
cost for $650$ KWh @ $$0.056582$ per KWh = $650 * 0.056582 = 36.7783$
$10 + 36.7783 = 46.7783$
Then, we can multiply the remaining consumption of power by $0.093983$
$c(p) = 46.7783 + 0.093983(p - 650)$
$c(p) = 46.7783 + 0.093983p - 61.08895$
$c(p) = 0.093983p - 14.31065$

For the third piece;
Basic service fee = $$10.00$
We have to "finish" with the first piece first
cost for $650$ KWh @ $$0.056582$ per KWh = $650 * 0.056582 = 36.7783$
$10 + 36.7783 = 46.7783$
Then we have to finish with the second piece next
$1000 - 650 = 350$
cost for $350$ KWh @ $$0.093983$ per KWh = $350 * 0.093983 = 32.89405$
$46.7783 + 32.89405 = 79.67235$
Then, we can multiply the remaining consumption of power by $0.097273$
$c(p) = 79.67235 + 0.097273(p - 1000)$
$c(p) = 79.67235 + 0.097273p - 97.273$
$c(p) = 0.097273p - 17.60065$

We can now write the piecewise function as:
$$ c(p) = \begin{cases} 0.056582p + 10; & \quad 0 \leq p \leq 650 \\[3ex] 0.093983p - 14.31065; & \quad 650 \lt p \leq 1000 \\[3ex] 0.097273p - 17.60065; & \quad p \gt 1000 \end{cases} $$ Let us recalculate all the questions using the Piecewise Function method.

(1.) 0 KWh falls in the first piece.

$ c(p) = 0.056582p + 10 \\[3ex] c(0) = 0.056582(0) + 10 \\[3ex] = 0 + 10 \\[3ex] = 10 \\[3ex] $ cost for $0$ KWh = $$10.00$

(2.) 300 KWh falls in the first piece.

$ c(p) = 0.056582p + 10 \\[3ex] c(300) = 0.056582(300) + 10 \\[3ex] = 16.9746 + 10 \\[3ex] = 26.9746 \\[3ex] = 26.97 \\[3ex] $ cost for $300$ KWh = $$26.97$

(3.) 700 KWh falls in the second piece.

$ c(p) = 0.093983p - 14.31065 \\[3ex] c(700) = 0.093983(700) - 14.31065 \\[3ex] = 65.7881 - 14.31065 \\[3ex] = 51.47745 \\[3ex] = 51.48 \\[3ex] $ cost for $700$ KWh = $$51.48$

(4.) 1000 KWh falls in the second piece.

$ c(p) = 0.093983p - 14.31065 \\[3ex] c(1000) = 0.093983(1000) - 14.31065 \\[3ex] = 93.983 - 14.31065 \\[3ex] = 79.67235 \\[3ex] = 79.67 \\[3ex] $ cost for $1000$ KWh = $$79.67$

(5.) 1200 KWh falls in the third piece.

$ c(p) = 0.097273p - 17.60065 \\[3ex] c(1200) = 0.097273(1200) - 17.60065 \\[3ex] = 116.7276 - 17.60065 \\[3ex] = 99.12695 \\[3ex] = 99.13 \\[3ex] $ cost for $1200$ KWh = $$99.13$

Which of the two methods do you prefer?
What are your reasons?
What are the pros and cons that you see for each method?
Do you have any other method for solving Piecewise Function applications?

---

---

As of the 7th day of July, 2018; the water rates by the Calhoun County Water Authority is found here

We shall focus on the Residential Rates. These rates exclude taxes.

                    It is also written here for you: 

                    First 3,000 Gallons:                $17.35 Minimum Per Month   

                    Next 2,000 Gallons:                 $5.24 per 1,000 Gallons  

                    Next 5,000 Gallons:                 $3.96 per 1,000 Gallons  

                    All over 10,000 Gallons:            $3.10 per 1,000 Gallons  
                    

---

Calculate the water rates for the following consumption of water.

(1.) $2500$ gallons
(2.) $3700$ gallons
(3.) $5000$ gallons
(4.) $7500$ gallons
(5.) $12000$ gallons
(6.) $4692$ gallons
(7.) $6456$ gallons

Solution: $1st$ Method: Manual/Arithmetic Method

This application has four pieces.
Let $g$ = gallons of water (in gallons)
Let $r$ = rate (in dollars per gallons)
(1.) $2500$ gallons falls in the first piece.
rate for $2500$ gallons @ $$17.35$ = $$17.35$

(2.) $3700$ gallons falls in the second piece.
Before we use the second piece, we have to go through the first piece first.
rate for $3000$ gallons @ $$17.35$ = $$17.35$
$3700 - 3000 = 700$
We need to find the rate for the remaining $700$ gallons
The first piece (for $3000$ gallons) is a constant rate. It is a flat fee.
However, the second piece is $$5.24$ per $1000$ gallons
The second piece is $$5.24$ per $1000$ (not per $700$) gallons

But, we have $700$ (not $1000$ gallons remaining). What do we do?
We have to use Proportional Reasoning Method to calculate the rate per gallons (rather than using the rate per thousand gallons)
Remember: per gallon means for $1$ gallon; and per $1000$ gallons means for a thousand gallons

Let us set up the Proportional Reasoning
Let $x$ be the cost per gallon

                                        dollars            gallons
                                        5.24                      1000
                                          x                         1
                    

This means that:
$$ \dfrac{5.24}{x} = \dfrac{1000}{1} \\[5ex] 1000 * x = 5.24 * 1 \\[3ex] 1000 * x = 5.24 \\[3ex] x = \dfrac{5.24}{1000} \\[5ex] x = 0.00524 $$ Similarly;
$$ \dfrac{3.96}{x} = \dfrac{1000}{1} \\[5ex] 1000 * x = 3.96 * 1 \\[3ex] 1000 * x = 3.96 \\[3ex] x = \dfrac{3.96}{1000} \\[5ex] x = 0.00396 $$ And;
$$ \dfrac{3.10}{x} = \dfrac{1000}{1} \\[5ex] 1000 * x = 3.1 * 1 \\[3ex] 1000 * x = 3.1 \\[3ex] x = \dfrac{3.1}{1000} \\[5ex] x = 0.0031 $$
Can we re-write the application?

                    First 3,000 Gallons:                $17.35 Minimum Per Month 

                    Next 2,000 Gallons:                 $0.00524 per gallon 

                    Next 5,000 Gallons:                 $0.00396 per gallon 

                    All over 10,000 Gallons:            $0.0031 per gallon  
                    

Ask students if they understood how the rates per gallon were calculated.

So, back to completing the second question:
rate for $700$ gallons @ $0.00524 per gallon = $0.00524 * 700$ = $$3.668$
Please do not approximate intermediate calculations especially if it deals with money!
rate for $3700$ gallons @ = 17.35 + 3.668 = 21.018
Now, you can round your final answer to the nearest cent.
NOTE: If your professor does not want you to round, do not round.
rate for $3700$ gallons = $$21.02$

(3.) $5000$ gallons falls in the second piece.
Before we use the second piece, we have to go through the first piece first.
rate for $3000$ gallons @ $$17.35$ = $$17.35$
$5000 - 3000 = 2000$
rate for $2000$ gallons @ $0.00524 per gallon = $0.00524 * 2000$ = $$10.48$
rate for $5000$ gallons @ = 17.35 + 10.48 = 27.83
rate for $5000$ gallons = $$27.83$

(4.) $7500$ gallons falls in the third piece.
Before we use the third piece, we have to go through the first and second pieces.
rate for $3000$ gallons @ $$17.35$ = $$17.35$
$7500 - 3000 = 4500$
rate for $2000$ gallons @ $0.00524 per gallon = $0.00524 * 2000$ = $$10.48$
$4500 - 2000 = 2500$
rate for $2500$ gallons @ $0.00396 per gallon = $0.00396 * 2500$ = $$9.90$
rate for $7500$ gallons @ = 17.35 + 10.48 + 9.90 = 37.73
rate for $7500$ gallons = $$37.73$

(5.) $12000$ gallons falls in the fourth piece.
Before we use the third piece, we have to go through the first, second, and third pieces.
rate for $3000$ gallons @ $$17.35$ = $$17.35$
$12000 - 3000 = 9000$
rate for $2000$ gallons @ $0.00524 per gallon = $0.00524 * 2000$ = $$10.48$
$9000 - 2000 = 7000$
rate for $5000$ gallons @ $0.00396 per gallon = $0.00396 * 5000$ = $$19.80$
$7000 - 5000 = 2000$
rate for $2000$ gallons @ $ per gallon = $0.0031 * 2000$ = $$6.20$
rate for $12000$ gallons @ = 17.35 + 10.48 + 19.80 + 6.20 = 53.83
rate for $12000$ gallons = $$53.83$

(6.) $4692$ gallons falls in the second piece.
Before we use the second piece, we have to go through the first piece first.
rate for $3000$ gallons @ $$17.35$ = $$17.35$
$4692 - 3000 = 1692$
rate for $1692$ gallons @ $0.00524 per gallon = $0.00524 * 1692$ = $$8.86608$
rate for $4692$ gallons @ = 17.35 + 8.86608 = 26.21608
rate for $4692$ gallons = $$26.22$

(7.) $6456$ gallons falls in the third piece.
Before we use the third piece, we have to go through the first and second pieces.
rate for $3000$ gallons @ $$17.35$ = $$17.35$
$6456 - 3000 = 3456$
rate for $2000$ gallons @ $0.00524 per gallon = $0.00524 * 2000$ = $$10.48$
$3456 - 2000 = 1456$
rate for $1456$ gallons @ $0.00396 per gallon = $0.00396 * 1456$ = $$5.76576$
rate for $6456$ gallons @ = 17.35 + 10.48 + 5.76576 = 33.59576
rate for $6456$ gallons = $$33.60$

Some students may ask if it is possible to have just one function that will find the rate for any gallon(s) of water?.
Or is it possible to find the rate for gallons of water that is contained in the second piece, without having to go through the first piece?

Solution: $2nd$ Method: Piecewise Function/Algebraic Method

What if we have to calculate the water rates for "several" gallons of water?
Do we have to solve this manually all the time? That will be time consuming!
We can write it as a piecewise function and use each function for the number of gallons that correspond to that piece.
Besides, writing it as a piecewise function helps us to write a computer program that will find the rate for any gallon of water.
This application has four pieces.
Let $g$ = gallons of water (in gallons)
Let $r$ = rate (in dollars per gallons)
$r = f(g)$
This can be written as: $r(g)$

For the first piece;
$r(g)$ = $$17.35$

For the second piece;
We have to "finish" with the first piece first
Then, we can multiply the remaining gallons of water by $0.00524$
$r(g) = 17.35 + 0.00524(g - 3000)$
$r(g) = 17.35 + 0.00524g - 15.72$
$r(g) = 0.00524g + 1.63$

For the third piece;
We have to "finish" the second piece first
Then, we can multiply the remaining gallons of water by $0.00396$
What is the complete gallons for the second piece? - It is $5000$
In other words, $5000$ is the end point for the second piece. $5000$ is included.
Let us find the rate for that end point, $5000$
$r(g) = 0.00524(5000) + 1.63$
$r(g) = 26.2 + 1.63 = 27.83$
So, $$27.83$ is the most that can be charged for the second piece.
Any remaining gallons over $5000$ would be multiplied by $0.00396$
$r(g) = 27.83 + 0.00396(g - 5000)$
$r(g) = 27.83 + 0.00396g - 19.8$
$r(g) = 0.00396g + 8.03$

For the fourth piece;
We have to "finish" the third piece first
Then, we can multiply the remaining gallons of water by $0.0031$
What is the complete gallons for the second piece? - It is $10000$
In other words, $10000$ is the end point for the third piece. $10000$ is included.
Let us find the rate for that end point, $10000$
$r(g) = 0.00396(10000) + 8.03$ $r(g) = 39.6 + 8.03 = 47.63$
So, $$47.63$ is the most that can be charged for the third piece.
Any remaining gallons over $10000$ would be multiplied by $0.0031$
$r(g) = 47.63 + 0.0031(g - 10000)$
$r(g) = 47.63 + 0.0031g - 31$
$r(g) = 0.0031g + 16.63$

We can now write the piecewise function as:
$$ r(g) = \begin{cases} $17.35; & \quad 0 \leq g \leq 3000 \\[2ex] 0.00524g + 1.63; & \quad 3000 \lt g \leq 5000 \\[2ex] 0.00396g + 8.03; & \quad 5000 \lt g \leq 10000 \\[2ex] 0.0031g + 16.63; & \quad g \gt 10000 \end{cases} $$ Let us recalculate all the questions using the Piecewise Function method.

(1.) $2500$ gallons falls in the first piece.
The rate for the first piece is $$17.35$
$\therefore$ the rate for $2500$ gallons of water = $$17.35$

(2.) $3700$ gallons falls in the second piece.
The rate for the second piece is $0.00524g + 1.63$
For $g = 3700$, $r = 0.00524(3700) + 1.63$
$r = 19.388 + 1.63$
$r = 21.018$
$\therefore$ the rate for $3700$ gallons of water = $$21.02$

(3.) $5000$ gallons falls in the second piece.
The rate for the second piece is $0.00524g + 1.63$
For $g = 5000$, $r = 0.00524(5000) + 1.63$
$r = 26.2 + 1.63$
$r = 27.83$
$\therefore$ the rate for $5000$ gallons of water = $$27.83$

(4.) $7500$ gallons falls in the third piece.
The rate for the third piece is $0.00396g + 8.03$
For $g = 7500$, $r = 0.00396(7500) + 8.03$
$r = 29.7 + 8.03$
$r = 37.73$
$\therefore$ the rate for $7500$ gallons of water = $$37.73$

(5.) $12000$ gallons falls in the fourth piece.
The rate for the fourth piece is $0.0031g + 16.63$
For $g = 12000$, $r = 0.0031(12000) + 16.63$
$r = 37.2 + 16.63$
$r = 53.83$
$\therefore$ the rate for $12000$ gallons of water = $$53.83$

(6.) $4692$ gallons falls in the second piece.
The rate for the second piece is $0.00524g + 1.63$
For $g = 4692$, $r = 0.00524(4692) + 1.63$
$r = 24.58608 + 1.63$
$r = 26.21608$
$\therefore$ the rate for $4692$ gallons of water = $$26.22$

(7.) $6456$ gallons falls in the third piece.
The rate for the third piece is $0.00396g + 8.03$
For $g = 6456$, $r = 0.00396(6456) + 8.03$
$r = 25.56576 + 8.03$
$r = 33.59576$
$\therefore$ the rate for $6456$ gallons of water = $$33.60$

Which of the two methods do you prefer?
What are your reasons?
What are the pros and cons that you see for each method?
Do you have any other method for solving Piecewise Function applications?

---

---

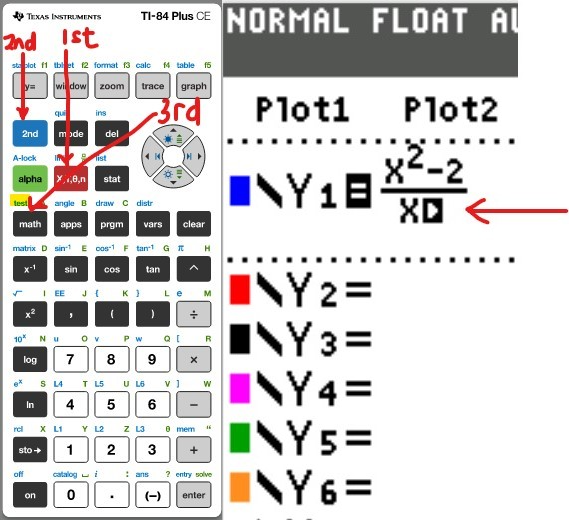
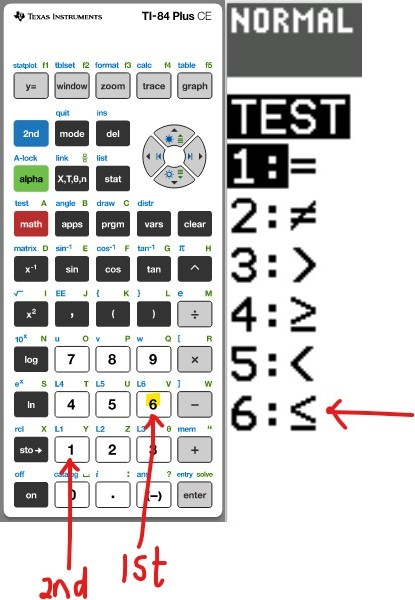
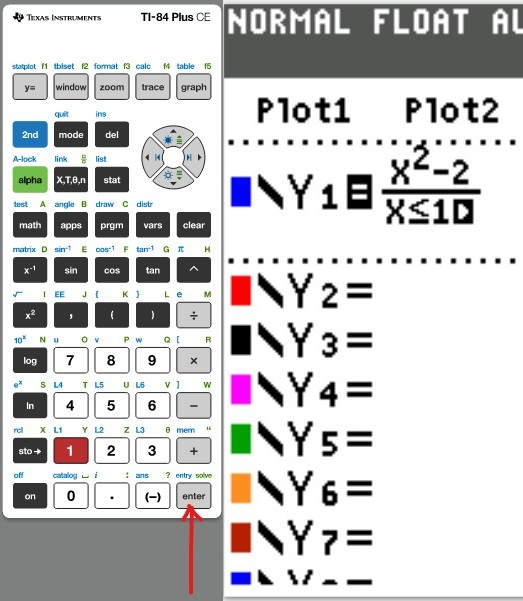
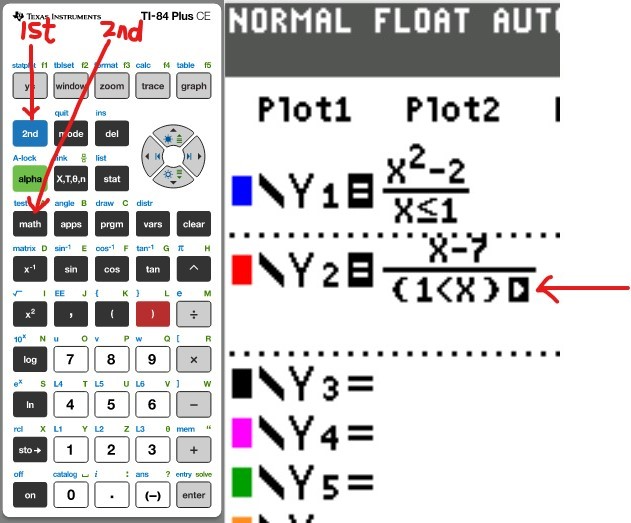
Another important real-world application of Piecewise Functions is in the filing of federal income taxes.
We shall illustrate this application by filing the "Single" option for the $2018$ federal tax return.
We shall design a calculator for these taxes.
We shall verify our calculations with the calculators of some tax companies.
For the simple calculations (only taxes), we shall verify it using the: calculator from TaxAct
Let us define some important terms used in Income Taxes.

The gross income is the total yearly income. This is the total income earned in a year.
It is the total pre-tax earnings for the year.
Let the gross income = $GI$

Sometimes, there are certain portions of the gross income that is not taxed.
In other words, there are certain untaxed portions of the gross income.
Those untaxed portions of the gross income are known as deductions or adjustments.
Let the adjustments = $A$
The difference between the gross income and the adjustments is known as the adjusted gross income
Let the adjusted gross income = $AGI$
The adjusted gross income is the income after allowable tax deductions.

The information used for the 2018 tax rates, standard deductions, and exemptions is found in these websites:
(1.) Bankrate
(2.) Forbes

Ask students to compare and contrast the two tables.

The information from the first website (Bankrate) is summarized here.
We shall work with this one first.

Tax Rate	Single	Head of household	Married Filing Jointly Or Qualifying Widow	Married Filing Separately
$10\%$	Up to $\$9,525$	Up to $\$13,600$	Up to $\$19,050$	Up to $\$9,525$
$12\%$	$\$9,526 \:\:to\:\: \$38,700$	$\$13,601 \:\:to\:\: \$51,800$	$\$19,051 \:\:to\:\: \$77,400$	$\$9,526 \:\:to\:\: \$38,700$
$22\%$	$\$38,701 \:\:to\:\: \$82,500$	$\$51,801 \:\:to\:\: \$82,500$	$\$77,401 \:\:to\:\: \$165,000$	$\$38,701 \:\:to\:\: \$82,500$
$24\%$	$\$82,501 \:\:to\:\: \$157,500$	$\$82,501 \:\:to\:\: \$157,500$	$\$165,001 \:\:to\:\: \$315,000$	$\$82,501 \:\:to\:\: \$157,000$
$32\%$	$\$157,501 \:\:to\:\: \$200,000$	$\$157,501 \:\:to\:\: \$200,000$	$\$315,001 \:\:to\:\: \$400,000$	$\$157,001 \:\:to\:\: \$200,000$
$35\%$	$\$200,001 \:\:to\:\: \$500,000$	$\$200,001 \:\:to\:\: \$500,000$	$\$400,001 \:\:to\:\: \$600,000$	$\$200,001 \:\:to\:\: \$300,000$
$37\%$	$\$500,001 \:\:or\:\: more$	$\$500,001 \:\:or\:\: more$	$\$600,001 \:\:or\:\: more$	$\$300,001 \:\:or\:\: more$

Let us calculate the taxes for the filing "Single" option.
We shall test each piece.

---

Calculate the taxes for single individuals whose taxable incomes are:

(1.) $\$7,000.00$
(2.) $\$12,575.00$
(3.) $\$43,750.00$
(4.) $\$120,327.00$
(5.) $\$165,428.00$
(6.) $\$234,543.00$
(7.) $\$700,712.00$

Simplify the percents.
$ 10\% = \dfrac{10}{100} = 0.1 \\[5ex] 12\% = \dfrac{12}{100} = 0.12 \\[5ex] 22\% = \dfrac{22}{100} = 0.22 \\[5ex] 24\% = \dfrac{24}{100} = 0.24 \\[5ex] 32\% = \dfrac{32}{100} = 0.32 \\[5ex] 35\% = \dfrac{35}{100} = 0.35 \\[5ex] 37\% = \dfrac{37}{100} = 0.37 $

Solution: $1st$ Method: Manual/Arithmetic Method

(1.) $\$7,000.00$ falls in the first piece.
tax for $\$7000.00$ income @ $10\%$ per $\$$ earned = $7000 * 0.1 = 700$
tax for taxable income of $\$7,000.00$ = $\$700.00$

(2.) $\$12,575.00$ falls in the second piece.
Before we use the second piece, we have to go through the first piece first.
First Piece for $\$9525.00$
$9525.00$ of the $12575.00$ is taxed at $10\%$
tax for $\$9525.00$ income @ $10\%$ per $\$$ earned = $9525.00 * 0.1 = 952.50$
We are done with the maximum taxable income that can be taxed at the first piece of $10\%$
We have to move on to the second piece.
$12575.00 - 9525.00 = 3050.00$
The rest of the $\$3050.00$ is taxed at $12\%$
Second Piece for $\$3050.00$
tax for $\$3050.00$ income @ $12\%$ per $\$$ earned = $3050.00 * 0.12 = 366.00$
$952.50 + 366.00 = 1318.50$
tax for taxable income of $\$12,575.00$ = $\$1,318.50$

(3.) $\$43,750.00$ falls in the third piece.
Before we use the third piece, we have to go through the first and second pieces.
First Piece for $\$9525.00$
$9525.00$ of the $12575.00$ is taxed at $10\%$
tax for $\$9525.00$ income @ $10\%$ per $\$$ earned = $9525.00 * 0.1 = 952.50$
We are done with the maximum taxable income that can be taxed at the first piece of $10\%$
We have to move on to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.

Student: So, do we need to subtract $9525.00$ from $43750.28$
Teacher: No, we do not.
Here is the thing.
We know already that $43750.28$ falls in the third tax bracket.
Student: That is correct.
Teacher: $9,525$ of that money is taxed at $10\%$
Student: Okay...
Teacher: Any money above $9525$ but not exceeding $38700$ is taxed at $12\%$
Not all the money (43750.00 - 9525 = 34225.00) is taxed at $12\%$
Let us look at it this way
For $43750.28$
$[0, 9525]$ is taxed at $10\%$
$(9525, 38700]$ is taxed at $12\%$
$(38700, 43750.28]$ is taxed at $22\%$
Do you realize the mistake that would have been made if $34225.00$ was taxed at $12\%$
Student: Yes, the U,S government would lose money.
Teacher: That is right...and we do not ...
Student: want them to lose money.
Teacher: Correct. That money could be used to help the poor.
Student: I hope they help poor people. There is a high rate of hunger and poverty in the world.
Teacher: I hope and pray so too.
So, as you can see:
The range of $9525 - 0 = 9525$ is taxed at $10\%$
Student: The range of $38700 - 9525 = 29175$ is taxed at $12\%$
Teacher: Correct! Go ahead...
Student: and the range of $43750.00 - 38700 = 5050.00$ is taxed at $22\%$ Teacher: Perfecto!

$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We have to move on to the third piece.
$43750.00 - 38700.00 = 5050.00$
The rest of the $\$5050.00$ is taxed at $22\%$
Third Piece for $\$14575.00$
tax for $\$5050.00$ income @ $22\%$ per $\$$ earned = $5050.00 * 0.22 = 1111.00$
$952.50 + 3501.00 + 1111.00 = 5564.50$
tax for taxable income of $\$43,750.00$ = $\$5,564.50$

(4.) $\$120, 327.00$ falls in the fourth piece.
Before we use the fourth piece, we have to go through the first, second, and third pieces.
First Piece for $\$9525.00$
$9525.00$ of the $12575.00$ is taxed at $10\%$
tax for $\$9525.00$ income @ $10\%$ per $\$$ earned = $9525.00 * 0.1 = 952.50$
We are done with the maximum taxable income that can be taxed at the first piece of $10\%$
We move to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.
$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We move to the third piece.
We need to calculate the range of taxable income that should be taxed at the third tax rate.
$82500.00 - 38700.00 = 43800.00$
$\$43800.00$ is taxed at $22\%$
Third Piece for $\$43800.00$
tax for $\$43800.00$ income @ $22\%$ per $\$$ earned = $43800.00 * 0.22 = 9636.00$
We are done with the maximum taxable income that can be taxed at the third piece of $22\%$
We move to the fourth piece.
$120327.00 - 82500.00 = 37827.00$
The rest of the $\$37827.00$ is taxed at $24\%$
Fourth Piece for $\$37827.00$
tax for $\$37827.00$ income @ $24\%$ per $\$$ earned = $37827.00 * 0.24 = 9078.48$
$952.50 + 3501.00 + 9636.00 + 9078.48 = 23167.98$
tax for taxable income of $\$120,327.00$ = $\$23,167.98$

(5.) $\$165, 428.00$ falls in the fifth piece.
Before we use the fifth piece, we have to go through the first, second, third, and fourth pieces.
First Piece for $\$9525.00$
$9525.00$ of the $12575.00$ is taxed at $10\%$
tax for $\$9525.00$ income @ $10\%$ per $\$$ earned = $9525.00 * 0.1 = 952.50$
We are done with the maximum taxable income that can be taxed at the first piece of $10\%$
We move to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.
$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We move to the third piece.
We need to calculate the range of taxable income that should be taxed at the third tax rate.
$82500.00 - 38700.00 = 43800.00$
$\$43800.00$ is taxed at $22\%$
Third Piece for $\$43800.00$
tax for $\$43800.00$ income @ $22\%$ per $\$$ earned = $43800.00 * 0.22 = 9636.00$
We are done with the maximum taxable income that can be taxed at the third piece of $22\%$
We move to the fourth piece.
We need to calculate the range of taxable income that should be taxed at the fourth tax rate.
$157500.00 - 82500.00 = 75000.00$
$\$75000.00$ is taxed at $24\%$
Fourth Piece for $\$75000.00$
tax for $\$75000.00$ income @ $24\%$ per $\$$ earned = $75000.00 * 0.24 = 18000.00$
We are done with the maximum taxable income that can be taxed at the fourth piece of $24\%$
We move to the fifth piece.
$165428.00 - 157500.00 = 7928.00$
The rest of the $\$7928.00$ is taxed at $32\%$
Fifth Piece for $\$7928.00$
tax for $\$7928.00$ income @ $32\%$ per $\$$ earned = $7928.00 * 0.32 = 2536.96$
$952.50 + 3501.00 + 9636.00 + 18000 + 2536.96 = 34626.46$
tax for taxable income of $\$165,428.00$ = $\$34,626.46$

(6.) $\$234,543.00$ falls in the sixth piece.
Before we use the sixth piece, we have to go through the first, second, third, fourth, and fifth pieces.
First Piece for $\$9525.00$
$9525.00$ of the $12575.00$ is taxed at $10\%$
tax for $\$9525.00$ income @ $10\%$ per $\$$ earned = $9525.00 * 0.1 = 952.50$
We are done with the maximum taxable income that can be taxed at the first piece of $10\%$
We move to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.
$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We move to the third piece.
We need to calculate the range of taxable income that should be taxed at the third tax rate.
$82500.00 - 38700.00 = 43800.00$
$\$43800.00$ is taxed at $22\%$
Third Piece for $\$43800.00$
tax for $\$43800.00$ income @ $22\%$ per $\$$ earned = $43800.00 * 0.22 = 9636.00$
We are done with the maximum taxable income that can be taxed at the third piece of $22\%$
We move to the fourth piece.
We need to calculate the range of taxable income that should be taxed at the fourth tax rate.
$157500.00 - 82500.00 = 75000.00$
$\$75000.00$ is taxed at $24\%$
Fourth Piece for $\$75000.00$
tax for $\$75000.00$ income @ $24\%$ per $\$$ earned = $75000.00 * 0.24 = 18000.00$
We are done with the maximum taxable income that can be taxed at the fourth piece of $24\%$
We move to the fifth piece.
We need to calculate the range of taxable income that should be taxed at the fifth tax rate.
$200000.00 - 157500.00 = 42500.00$
$\$42500.00$ is taxed at $32\%$
Fifth Piece for $\$42500.00$
tax for $\$42500.00$ income @ $32\%$ per $\$$ earned = $42500.00 * 0.32 = 13600.00$
We are done with the maximum taxable income that can be taxed at the fifth piece of $32\%$
We move to the sixth piece.
$234543.00 - 200000.00 = 34543.00$
The rest of the $\$34543.00$ is taxed at $35\%$
Sixth Piece for $\$34543.00$
tax for $\$34543.00$ income @ $35\%$ per $\$$ earned = $34543.00 * 0.35 = 12090.05$
$952.50 + 3501.00 + 9636.00 + 18000 + 13600 + 12090.05 = 57779.55$
tax for taxable income of $\$234,543.00$ = $\$57,779.55$

(7.) $\$700,712.00$ falls in the seventh piece.
Before we use the seventh piece (last piece), we have to go through the previous six pieces in order.
First Piece for $\$9525.00$
$9525.00$ of the $12575.00$ is taxed at $10\%$
tax for $\$9525.00$ income @ $10\%$ per $\$$ earned = $9525.00 * 0.1 = 952.50$
We are done with the maximum taxable income that can be taxed at the first piece of $10\%$
We move to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.
$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We move to the third piece.
We need to calculate the range of taxable income that should be taxed at the third tax rate.
$82500.00 - 38700.00 = 43800.00$
$\$43800.00$ is taxed at $22\%$
Third Piece for $\$43800.00$
tax for $\$43800.00$ income @ $22\%$ per $\$$ earned = $43800.00 * 0.22 = 9636.00$
We are done with the maximum taxable income that can be taxed at the third piece of $22\%$
We move to the fourth piece.
We need to calculate the range of taxable income that should be taxed at the fourth tax rate.
$157500.00 - 82500.00 = 75000.00$
$\$75000.00$ is taxed at $24\%$
Fourth Piece for $\$75000.00$
tax for $\$75000.00$ income @ $24\%$ per $\$$ earned = $75000.00 * 0.24 = 18000.00$
We are done with the maximum taxable income that can be taxed at the fourth piece of $24\%$
We move to the fifth piece.
We need to calculate the range of taxable income that should be taxed at the fifth tax rate.
$200000.00 - 157500.00 = 42500.00$
$\$42500.00$ is taxed at $32\%$
Fifth Piece for $\$42500.00$
tax for $\$42500.00$ income @ $32\%$ per $\$$ earned = $42500.00 * 0.32 = 13600.00$
We are done with the maximum taxable income that can be taxed at the fifth piece of $32\%$
We move to the sixth piece.
We need to calculate the range of taxable income that should be taxed at the sixth tax rate.
$500000.00 - 200000.00 = 300000.00$
$\$300000.00$ is taxed at $35\%$
Sixth Piece for $\$300000.00$
tax for $\$300000.00$ income @ $35\%$ per $\$$ earned = $300000.00 * 0.35 = 105000.00$
We are done with the maximum taxable income that can be taxed at the sixth piece of $35\%$
We move to the seventh piece.
$700712.00 - 500000.00 = 200712.00$
The rest of the $\$200712.00$ is taxed at $37\%$
Seventh Piece for $\$200712.00$
tax for $\$200712.00$ income @ $37\%$ per $\$$ earned = $200712.00 * 0.37 = 74263.44$
$952.50 + 3501.00 + 9636.00 + 18000 + 13600 + 105000 + 74263.44 = 224952.94$
tax for taxable income of $\$700,712.00$ = $\$224,952.94$

Some students may ask if it is possible to have just one function that will calculate the tax for any taxable income.
Or is it possible to find the tax for a taxable income that falls in the second piece, without having to go through the first piece?

Those are really interesting questions!
That is one of the reasons for studying piecewise functions ☺☺☺

Please specify the importance of not rounding intermediate calculations.
Please specify the importance of rounding only the final answer to two decimal place (because it is dollars and cents).

Solution: $2nd$ Method: Piecewise Function/Algebraic Method

What if we have to calculate the taxes for "several" taxable incomes?
Do we have to solve this manually all the time? That will be time consuming!
We can write it as a piecewise function and use each function to calculate the taxes that corresponds to each taxable income.
Besides, writing it as a piecewise function helps us to write a computer program that will calculate the taxes for any amount of taxable income.

Define the variables.
Let $p$ = taxable income (in $\$$)
Let $t$ = taxes (in $\$$)
The taxes paid is a function of the income earned.
Taxes is the dependent variable.
Taxable income is the independent variable.
$t = f(p)$
We can also write is as $t(p)$
This application has seven pieces.

For the first piece;
tax for $\$p$ income @ $10\%$ per $\$$ earned = $p * 0.1 = 0.1p$
$t(p) = 0.1p$

For the second piece;
We have to "finish" with the first piece first
First Piece for $\$9525.00$
tax for $\$9525$ income @ $10\%$ per $\$$ earned = $9525 * 0.1 = 952.5$
Then, we move to the second piece.
Second Piece for $\$p - 9525.00$
The remaining income, $(p - 9525)$ is taxed at $12\%$
So, we have to multiply the remaining income by $0.12$
$t(p) = 952.5 + 0.12(p - 9525)$
$t(p) = 952.5 + 0.12p - 1143$
$t(p) = 0.12p - 190.5$

For the third piece;
We have to "finish" with the first and second pieces
First Piece for $\$9525.00$
tax for $\$9525$ income @ $10\%$ per $\$$ earned = $9525 * 0.1 = 952.5$
Then, we move to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.
Please review the scenario in the Manual/Arithmetic Method
$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We have to move on to the third piece.
Third Piece for $\$p - 38700.00$
The remaining income, $(p - 38700)$ is taxed at $22\%$
So, we have to multiply the remaining income by $0.22$
$t(p) = 952.5 + 3501 + 0.22(p - 38700)$
$t(p) = 952.5 + 3501 + 0.22p - 8514$
$t(p) = 0.22p - 4060.5$

For the fourth piece;
We have to "finish" with the first, second, and third pieces
First Piece for $\$9525.00$
tax for $\$9525$ income @ $10\%$ per $\$$ earned = $9525 * 0.1 = 952.5$
Then, we move to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.
Please review the scenario in the Manual/Arithmetic Method
$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We move to the third piece.
We need to calculate the range of taxable income that should be taxed at the third tax rate.
$82500.00 - 38700.00 = 43800.00$
$\$43800.00$ is taxed at $22\%$
Third Piece for $\$43800.00$
tax for $\$43800.00$ income @ $22\%$ per $\$$ earned = $43800.00 * 0.22 = 9636.00$
We are done with the maximum taxable income that can be taxed at the second piece of $22\%$
We move to the fourth piece.
Fourth Piece for $\$p - 82500.00$
The remaining income, $(p - 82500)$ is taxed at $24\%$
So, we have to multiply the remaining income by $0.24$
$t(p) = 952.5 + 3501 + + 9636 + 0.24(p - 82500)$
$t(p) = 952.5 + 3501 + 9636 + 0.24p - 19800$
$t(p) = 0.24p - 5710.5$

For the fifth piece;
We have to "finish" with the first, second, third, and fourth pieces
First Piece for $\$9525.00$
tax for $\$9525$ income @ $10\%$ per $\$$ earned = $9525 * 0.1 = 952.5$
Then, we move to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.
Please review the scenario in the Manual/Arithmetic Method
$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We move to the third piece.
We need to calculate the range of taxable income that should be taxed at the third tax rate.
$82500.00 - 38700.00 = 43800.00$
$\$43800.00$ is taxed at $22\%$
Third Piece for $\$43800.00$
tax for $\$43800.00$ income @ $22\%$ per $\$$ earned = $43800.00 * 0.22 = 9636.00$
We are done with the maximum taxable income that can be taxed at the third piece of $22\%$
We move to the fourth piece.
We need to calculate the range of taxable income that should be taxed at the fourth tax rate.
$157500.00 - 82500.00 = 75000.00$
$\$75000.00$ is taxed at $24\%$
Fourth Piece for $\$75000.00$
tax for $\$75000.00$ income @ $24\%$ per $\$$ earned = $75000.00 * 0.24 = 18000.00$
We are done with the maximum taxable income that can be taxed at the fourth piece of $24\%$
We move to the fifth piece.
Fifth Piece for $\$p - 157500.00$
The remaining income, $(p - 157500)$ is taxed at $32\%$
So, we have to multiply the remaining income by $0.32$
$t(p) = 952.5 + 3501 + + 9636 + 18000 + 0.32(p - 157500)$
$t(p) = 952.5 + 3501 + 9636 + 18000 + 0.32p - 50400$
$t(p) = 0.32p - 18310.5$

For the sixth piece;
We have to "finish" with the first, second, third, fourth, and fifth pieces
First Piece for $\$9525.00$
tax for $\$9525$ income @ $10\%$ per $\$$ earned = $9525 * 0.1 = 952.5$
Then, we move to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.
Please review the scenario in the Manual/Arithmetic Method
$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We move to the third piece.
We need to calculate the range of taxable income that should be taxed at the third tax rate.
$82500.00 - 38700.00 = 43800.00$
$\$43800.00$ is taxed at $22\%$
Third Piece for $\$43800.00$
tax for $\$43800.00$ income @ $22\%$ per $\$$ earned = $43800.00 * 0.22 = 9636.00$
We are done with the maximum taxable income that can be taxed at the third piece of $22\%$
We move to the fourth piece.
We need to calculate the range of taxable income that should be taxed at the fourth tax rate.
$157500.00 - 82500.00 = 75000.00$
$\$75000.00$ is taxed at $24\%$
Fourth Piece for $\$75000.00$
tax for $\$75000.00$ income @ $24\%$ per $\$$ earned = $75000.00 * 0.24 = 18000.00$
We are done with the maximum taxable income that can be taxed at the fourth piece of $24\%$
We move to the fifth piece.
We need to calculate the range of taxable income that should be taxed at the fifth tax rate.
$200000.00 - 157500.00 = 42500.00$
$\$42500.00$ is taxed at $32\%$
Fifth Piece for $\$42500.00$
tax for $\$42500.00$ income @ $32\%$ per $\$$ earned = $42500.00 * 0.32 = 13600.00$
We are done with the maximum taxable income that can be taxed at the fifth piece of $32\%$
We move to the sixth piece.
Sixth Piece for $\$p - 200000.00$
The remaining income, $(p - 200000)$ is taxed at $35\%$
So, we have to multiply the remaining income by $0.35$
$t(p) = 952.5 + 3501 + + 9636 + 18000 + 13600 + 0.35(p - 200000)$
$t(p) = 952.5 + 3501 + 9636 + 18000 + 13600 + 0.35p - 70000$
$t(p) = 0.35p - 24310.5$

For the seventh piece;
We have to "finish" with the previous six pieces in order
First Piece for $\$9525.00$
tax for $\$9525$ income @ $10\%$ per $\$$ earned = $9525 * 0.1 = 952.5$
Then, we move to the second piece.
We need to calculate the range of taxable income that should be taxed at the second tax rate.
Please review the scenario in the Manual/Arithmetic Method
$38700.00 - 9525.00 = 29175.00$
$\$29175.00$ is taxed at $12\%$
Second Piece for $\$29175.00$
tax for $\$29175.00$ income @ $12\%$ per $\$$ earned = $29175.00 * 0.12 = 3501.00$
We are done with the maximum taxable income that can be taxed at the second piece of $12\%$
We move to the third piece.
We need to calculate the range of taxable income that should be taxed at the third tax rate.
$82500.00 - 38700.00 = 43800.00$
$\$43800.00$ is taxed at $22\%$
Third Piece for $\$43800.00$
tax for $\$43800.00$ income @ $22\%$ per $\$$ earned = $43800.00 * 0.22 = 9636.00$
We are done with the maximum taxable income that can be taxed at the third piece of $22\%$
We move to the fourth piece.
We need to calculate the range of taxable income that should be taxed at the fourth tax rate.
$157500.00 - 82500.00 = 75000.00$
$\$75000.00$ is taxed at $24\%$
Fourth Piece for $\$75000.00$
tax for $\$75000.00$ income @ $24\%$ per $\$$ earned = $75000.00 * 0.24 = 18000.00$
We are done with the maximum taxable income that can be taxed at the fourth piece of $24\%$
We move to the fifth piece.
We need to calculate the range of taxable income that should be taxed at the fifth tax rate.
$200000.00 - 157500.00 = 42500.00$
$\$42500.00$ is taxed at $32\%$
Fifth Piece for $\$42500.00$
tax for $\$42500.00$ income @ $32\%$ per $\$$ earned = $42500.00 * 0.32 = 13600.00$
We are done with the maximum taxable income that can be taxed at the fifth piece of $32\%$
We move to the sixth piece.
We need to calculate the range of taxable income that should be taxed at the sixth tax rate.
$500000.00 - 200000.00 = 300000.00$
$\$300000.00$ is taxed at $35\%$
Sixth Piece for $\$300000.00$
tax for $\$300000.00$ income @ $35\%$ per $\$$ earned = $300000.00 * 0.35 = 105000.00$
We are done with the maximum taxable income that can be taxed at the sixth piece of $35\%$
We move to the seventh piece.
Seventh Piece for $\$p - 500000.00$
The remaining income, $(p - 500000)$ is taxed at $37\%$
So, we have to multiply the remaining income by $0.37$
$t(p) = 952.5 + 3501 + + 9636 + 18000 + 13600 + 105000 + 0.37(p - 500000)$
$t(p) = 952.5 + 3501 + 9636 + 18000 + 13600 + 105000 + 0.37p - 185000$
$t(p) = 0.37p - 34310.5$

We can now write the piecewise function as:
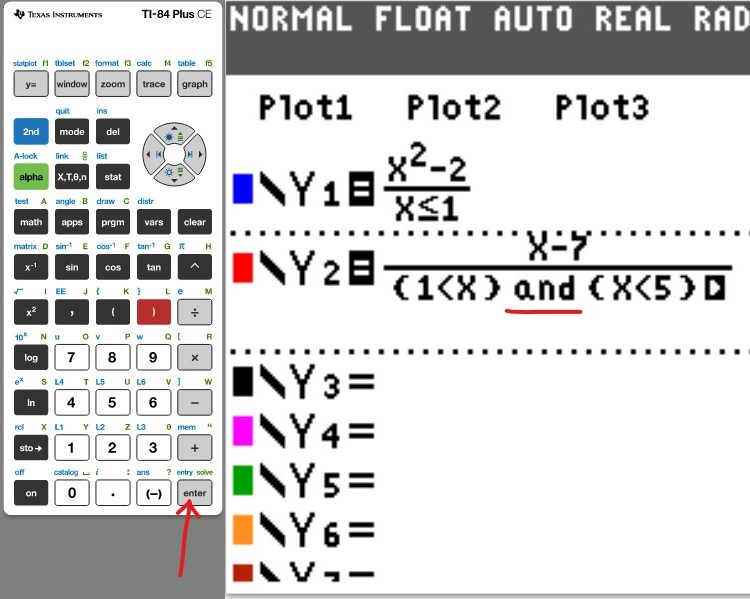
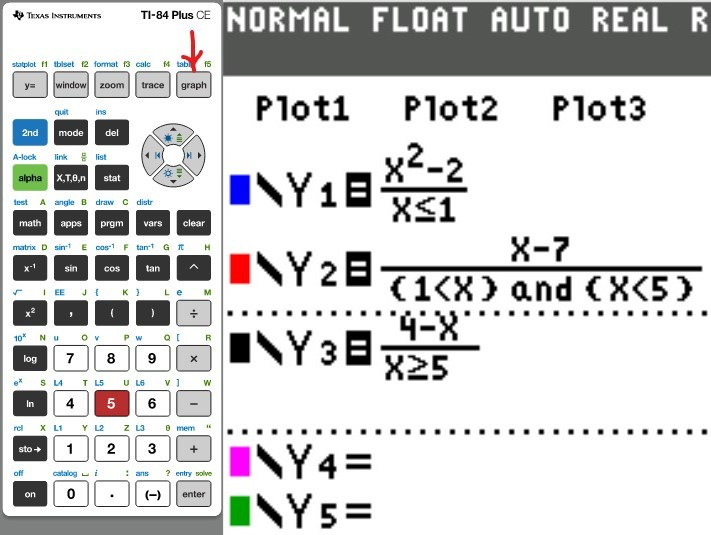
$$ t(p) = \begin{cases} \\[3ex] 0.1p; & \quad 0 \leq p \leq 9525 \\[3ex] 0.12p - 190.5; & \quad 9525 \lt p \leq 38700 \\[3ex] 0.22p - 4060.5; & \quad 38700 \lt p \leq 82500 \\[3ex] 0.24p - 5710.5; & \quad 82500 \lt p \leq 157500 \\[3ex] 0.32p - 18310.5; & \quad 157500 \lt p \leq 200000 \\[3ex] 0.35p - 24310.5; & \quad 200000 \lt p \leq 500000 \\[3ex] 0.37p - 34310.5; & \quad p \gt 500000 \end{cases} $$ Let us recalculate all the questions using the Piecewise Function method.

(1.) $\$7,000.00$ falls in the first piece.

$ t(p) = 0.1p \\[3ex] t(7000) = 0.1(7000) \\[3ex] = 700 \\[3ex] $ tax for taxable income of $\$7,000.00$ = $\$700.00$

(2.) $\$12,575.00$ falls in the second piece.

$ t(p) = 0.12p - 190.5 \\[3ex] t(12575) = 0.12(12575) - 190.5 \\[3ex] = 1509 - 190.5 \\[3ex] = 1318.5 \\[3ex] $ tax for taxable income of $\$12,575.00$ = $\$1,318.50$

(3.) $\$43,750.00$ falls in the third piece.

$ t(p) = 0.22p - 4060.5 \\[3ex] t(43750) = 0.22(43750) - 4060.5 \\[3ex] = 9625 - 4060.5 \\[3ex] = 5564.5 \\[3ex] $ tax for taxable income of $\$43,750.00$ = $\$5,564.50$

(4.) $\$120,327.00$ falls in the fourth piece.

$ t(p) = 0.24p - 5710.5 \\[3ex] t(120327) = 0.24(120327) - 5710.5 \\[3ex] = 28878.48 - 5710.5 \\[3ex] = 23167.98 \\[3ex] $ tax for taxable income of $\$120,327.00$ = $\$23,167.98$

(5.) $\$165,428.00$ falls in the fifth piece.

$ t(p) = 0.32p - 18310.5 \\[3ex] t(165428) = 0.32(165428) - 18310.5 \\[3ex] = 52936.96 - 18310.5 \\[3ex] = 34626.46 \\[3ex] $ tax for taxable income of $\$165,428.00$ = $\$34,626.46$

(6.) $\$234,543.00$ falls in the sixth piece.

$ t(p) = 0.35p - 24310.5 \\[3ex] t(234543) = 0.35(234543) - 24310.5 \\[3ex] = 82090.05 - 24310.5 \\[3ex] = 57779.55 \\[3ex] $ tax for taxable income of $\$234,543.00$ = $\$57,779.55$

(7.) $\$700,712.00$ falls in the seventh piece.

$ t(p) = 0.37p - 34310.5 \\[3ex] t(700712) = 0.37(700712) - 34310.5 \\[3ex] = 259263.44 - 34310.5 \\[3ex] = 224952.94 \\[3ex] $ tax for taxable income of $\$700,712.00$ = $\$224,952.94$

Ask students their preferred method - solving it manually or solving it by piecewise function.
They should give reasons for their answers.
Ask students if any of them can come up with another method besides the two methods already discussed.

Before we develop the calculator for the 2018 Federal Income Tax, we need to write the Piecewise Functions for the other filing options.
We can ask the user to select any of the filing options to calculate the tax.
If you follow the example for the Single filing option, you should get the same results that I get.
Please verify your results with my own. If you find any discrepancy even by one cent, please let me know.

The Piecewise Function for the Head of Household is: $$ t(p) = \begin{cases} \\[3ex] 0.1p; & \quad 0 \leq p \leq 13600 \\[3ex] 0.12p - 272; & \quad 13600 \lt p \leq 51800 \\[3ex] 0.22p - 5452; & \quad 51800 \lt p \leq 82500 \\[3ex] 0.24p - 7102; & \quad 82500 \lt p \leq 157500 \\[3ex] 0.32p - 19702; & \quad 157500 \lt p \leq 200000 \\[3ex] 0.35p - 25702; & \quad 200000 \lt p \leq 500000 \\[3ex] 0.37p - 35702; & \quad p \gt 500000 \end{cases} $$

The Piecewise Function for the Married Filing Jointly or Qualifying Widow is: $$ t(p) = \begin{cases} \\[3ex] 0.1p; & \quad 0 \leq p \leq 19050 \\[3ex] 0.12p - 381; & \quad 19050 \lt p \leq 77400 \\[3ex] 0.22p - 8121; & \quad 77400 \lt p \leq 165000 \\[3ex] 0.24p - 11421; & \quad 165000 \lt p \leq 315000 \\[3ex] 0.32p - 36621; & \quad 315000 \lt p \leq 400000 \\[3ex] 0.35p - 48621; & \quad 400000 \lt p \leq 600000 \\[3ex] 0.37p - 60621; & \quad p \gt 600000 \end{cases} $$

The Piecewise Function for the Married Filing Separately is: $$ t(p) = \begin{cases} \\[3ex] 0.1p; & \quad 0 \leq p \leq 9525 \\[3ex] 0.12p - 190.5; & \quad 9525 \lt p \leq 38700 \\[3ex] 0.22p - 4060.5; & \quad 38700 \lt p \leq 82500 \\[3ex] 0.24p - 5710.5; & \quad 82500 \lt p \leq 157000 \\[3ex] 0.32p - 18270.5; & \quad 157000 \lt p \leq 200000 \\[3ex] 0.35p - 24270.5; & \quad 200000 \lt p \leq 300000 \\[3ex] 0.37p - 30270.5; & \quad p \gt 300000 \end{cases} $$

Which of the two methods do you prefer?
What are your reasons?
What are the pros and cons that you see for each method?
Do you have any other method for solving Piecewise Function applications?

---

---

To graph a piecewise function:

(1.) Write the Table of Values for each piece

(2.) Make sure the end points for the domain of each piece are indicated in each Table of Value

(3.) Specify whether each end point is defined or undefined.

(4.) Plot each Table of Values on a graph.
Any end point that is defined should be labeled as a closed circle. This means that the end point is included in the domain for that piece.
Any end point that is not defined should be labeled as an open circle. This means that the end point is not included in the domain for that piece.

Let us do an example.

Example 1: ACT Which of the following is the graph of the function f(x) defined below?

$ f(x) = \begin{cases} x^2 - 2 \enspace \text{for} \enspace x \le 1 \\[3ex] x - 7 \enspace \text{for} \enspace 1 \lt x \lt 5 \\[3ex] 4 - x \enspace \text{for} \enspace x \ge 5 \end{cases} \\[7ex] $

Show/Hide Answer

We can sketch the graph:
(1.) Manually on a graph paper
(2.) Using a graphing calculator/technology.

Let us sketch the graph using the Texas Instrument (TI) Graphing Calculator
You may use any of these TI calculators:
TI-83 Plus
TI-84 Plus series
TI-Nspire CX series
TI-89 Titanium
TI-73 Explorer

The first thing we need to do is to reset the Random Access Memory (RAM).
This will clear everything that was initially stored by a previous user.
Also, after each problem, it is recommended that you reset the calculator.
NOTE: Please go over each step. Do not skip.

Reset the Calculator
(1.)

(2.)

(3.)

(4.)



Graph Example 1
Step 1:


Step 2:
Enter the function and the domain of each piece
There are at least two approaches that we can use here:
(A.) First Approach: As a quotient of the function and the domain for each piece
This means $\dfrac{function}{domain}$ for each piece

This is the $\dfrac{n}{d}$ = $\dfrac{numerator}{denominator}$

Let us begin with the first piece
(2a.)

(2b.)

NOTE:
(1.) If you have a TI-84 Plus calculator, the $\dfrac{n}{d}$ is found by: MATH ⟩⟩ NUM ⟩⟩ D:n/d
(2.) If you have a TI-83 calculator, you can use the division button: ÷

(2c.)

(2d.)

(2e.)

(2f.)

Step 3:
Enter the function and the domain of the second piece
(3a.)

The domain of the second piece is a compound inequality
For compound ineuqlities, we use the logical connectives: and and or depending on the compound inequality
For the domain of this piecewise function, we shall use the logical connective: and to join the two simple inequalities
(3b.)

(3c.)

Step 4:
Enter the function and the domain of the third piece


Step 5:
Graph the piecewise function




We can do this another way.
(B.) Second Approach: As a sum of the products of the function and the domain of all the pieces
We write this sum as a single function (in $Y_1$) rather than in three different functions as we did in the first approach. So, let us reset the calculator.
The graph of this approach is the same as the graph of the first approach.

Step 2:
Enter the function and the domain of each piece
Enclose the function in parenthesis
Enclose the domain in parenthesis
Write as a sum of products


This is the equation that was written: $Y_1 = (X^2 - 2) * (X \le 1) + (X - 7) * (1 \lt X \;\;and\;\; X \lt 5) + (4 - X) * (X \ge 5)$
NOTE: The mutiplication, * and the addition, + symbols are required.

Step 3:

The greatest integer function is also called the floor function.

The greatest integer of a number is defined as the greatest integer less than or equal to that number.

The greatest integer of a number, say x is denoted by ${\lfloor x \rfloor}$ or $[\![ x ]\!]$ or int(x)

$\mathbb{Z}$ is the set of all integers.
Say we have a decimal: $\large x.y$;
$x$ is the integer part.

$$ {\lfloor x \rfloor} = \begin{cases} x; & \quad x \: \epsilon \: \mathbb{Z} \\[3ex] x; & \quad x.y > 0 \\[3ex] x - 1; & \quad x.y < 0 \end{cases} $$

---

The greatest integer of $\:$ =

Calculate

The least integer function is also called the ceiling function.

The least integer of a number is defined as the least integer greater than or equal to that number.

The least integer of a number, say $x$ is denoted by ${\lceil x \rceil}$ or $]\!]x[\![$

$\mathbb{Z}$ is the set of all integers.

Say we have a decimal: $\large x.y$;
$x$ is the integer part.

$$ {\lceil x \rceil} = \begin{cases} x, & \quad \text{if }\: x \: \epsilon \: \mathbb{Z} \\[2ex] x + 1, & \quad \text{if }\: x.y > 0 \\[2ex] x, & \quad \text{if }\: x.y < 0 \end{cases} $$

Did you notice we wrote this piecewise function in another way? It is still acceptable this way.

---

The least integer of $\:$ =

Calculate

The absolute value function is sometimes called the modulus function. (not modulo function)

The absolute value of a number is defined as the magnitude of the number regardless of sign.

This implies that the absolute value of a number must either be zero, or positive.

The number can be negative, zero, or positive.

However, the absolute value cannot be negative.

It can either be zero (if the number is zero), or positive (if the number is negative or positive).

The absolute value of a number, say $x$ is denoted by $|x|$

$$ |x| = \begin{cases} -x; & \quad x< 0 \\[2ex] x; & \quad x≥ 0 \end{cases} $$

---

The absolute value of $\:$ =

Calculate