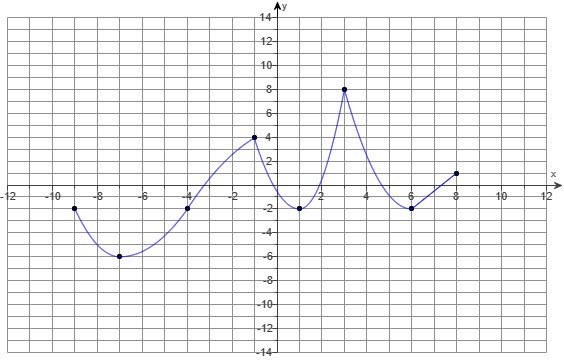
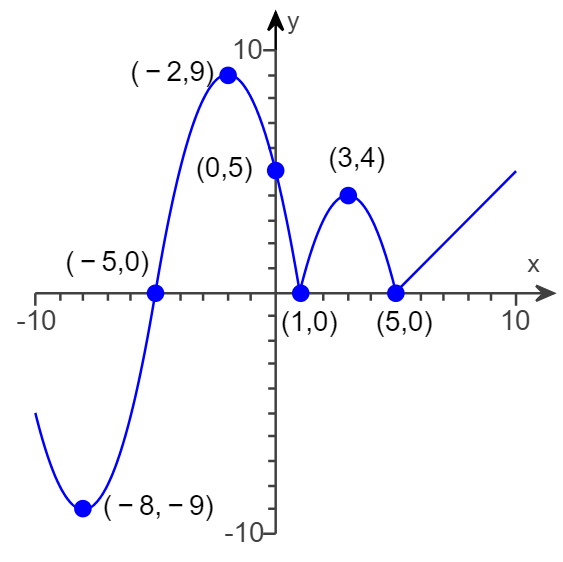
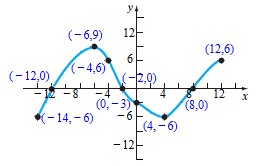
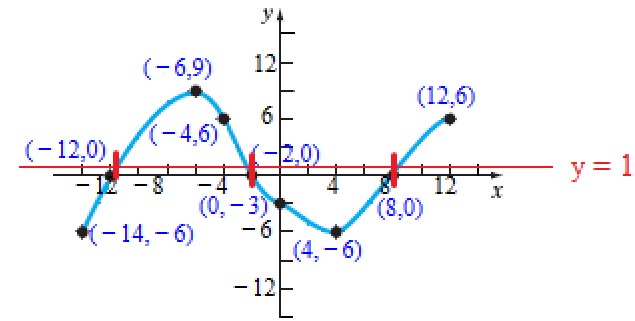
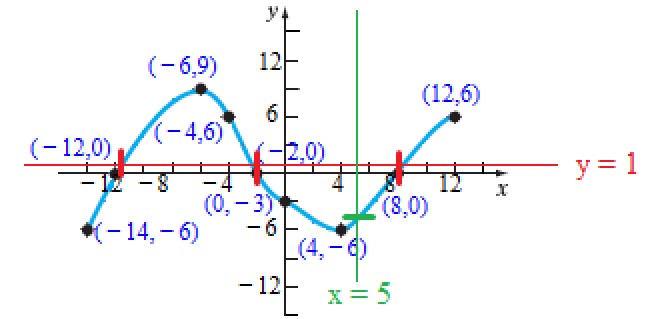
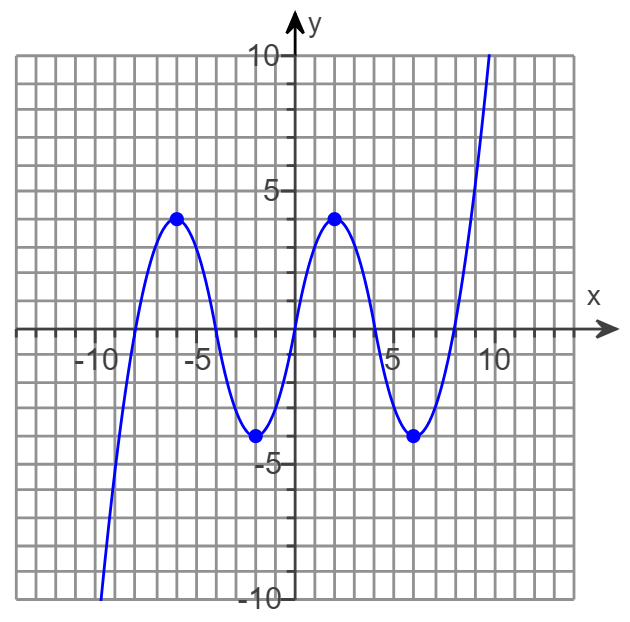
(1.) Analyze the graph of the function based on increasing, decreasing, and constant intervals.
In other words: Based on the graph, at what intervals of x does the function, y increase. decrease, or remain constant?
$ y \uparrow \;\;\;for\;\;\; x \in (-8, -2) \cup (0, 2) \cup (5, 7) \\[3ex] y \downarrow \;\;\;for\;\;\; x \in (-10, -8) \cup (-2, 0) \cup (2, 5) $
In other words: Based on the graph, at what intervals of x does the function, y increase. decrease, or remain constant?

$ y \uparrow \;\;\;for\;\;\; x \in (-8, -2) \cup (0, 2) \cup (5, 7) \\[3ex] y \downarrow \;\;\;for\;\;\; x \in (-10, -8) \cup (-2, 0) \cup (2, 5) $
(2.) State whether the following statements are true or false.
(a.) Every graph represents a function.
(b.) The graph of a function y = f(x) always crosses the y-axis.
(c.) The point (−7, −6) is on the graph of the equation x = 4y − 5.
(d.) The y-intercept of the graph of the function $y = f(x)$, whose domain is all real numbers, is $f(0)$.
(a.) This statement is false because of the Vertical Line Test.
The statement is false because a graph that crosses the y-axis two times does not represent a function.
If the vertical line intersects the graph at only one point, the graph is a function because no input, x has more than one output, y.
If the vertical line intersects the graph at more than point, the graph is not a function because there is at least an input, x that has more than one output, y.
The Vertical Line Test states that if a vertical line is drawn through the graph of a set of points in the rectangular coordinate system, the graph is a function if and only if the vertical line intersects the graph at only one point.
If a graph crosses the y-axis more than one time, it has failed the Vertical Line Test because it means that there is at least an input, x that has more than one output, y.
(b.) On the y-axis, the x-value is zero.
Some functions have domains that do not include zeros. For example, the parent function of a rational function is $y = \dfrac{1}{x}$
For that function, the graph will never cross the y-axis because the vertical asymptote, $x = 0$ is the y-axis
There are some graphs that do not cross the y-axis. Hence, te graph of a function does not always cross the y-axis
The statement is false.
$ (c.) \\[3ex] x = 4y - 5 \\[3ex] (-7, -6) \implies \\[3ex] x = -7 \\[3ex] y = -6 \\[3ex] \implies \\[3ex] -7 \stackrel{?}{=} 4(-6) - 5 \\[3ex] -7 \stackrel{?}{=} -24 - 5 \\[3ex] -7 \ne -29 \\[3ex] $ The point (−7, −6) is not on the graph of the equation x = 4y − 5.
(d.) The statement is true.
For all real number domain:
To find the y-intercept:
set x to 0 and
solve for y
Hence: for $y = f(x)$,
$y = f(0)$ is the value of the y-intercept.
But, please note that y-intercept is a point.
So, the y-intercept = $(0, y-value)$
(a.) Every graph represents a function.
(b.) The graph of a function y = f(x) always crosses the y-axis.
(c.) The point (−7, −6) is on the graph of the equation x = 4y − 5.
(d.) The y-intercept of the graph of the function $y = f(x)$, whose domain is all real numbers, is $f(0)$.
(a.) This statement is false because of the Vertical Line Test.
The statement is false because a graph that crosses the y-axis two times does not represent a function.
If the vertical line intersects the graph at only one point, the graph is a function because no input, x has more than one output, y.
If the vertical line intersects the graph at more than point, the graph is not a function because there is at least an input, x that has more than one output, y.
The Vertical Line Test states that if a vertical line is drawn through the graph of a set of points in the rectangular coordinate system, the graph is a function if and only if the vertical line intersects the graph at only one point.
If a graph crosses the y-axis more than one time, it has failed the Vertical Line Test because it means that there is at least an input, x that has more than one output, y.
(b.) On the y-axis, the x-value is zero.
Some functions have domains that do not include zeros. For example, the parent function of a rational function is $y = \dfrac{1}{x}$
For that function, the graph will never cross the y-axis because the vertical asymptote, $x = 0$ is the y-axis
There are some graphs that do not cross the y-axis. Hence, te graph of a function does not always cross the y-axis
The statement is false.
$ (c.) \\[3ex] x = 4y - 5 \\[3ex] (-7, -6) \implies \\[3ex] x = -7 \\[3ex] y = -6 \\[3ex] \implies \\[3ex] -7 \stackrel{?}{=} 4(-6) - 5 \\[3ex] -7 \stackrel{?}{=} -24 - 5 \\[3ex] -7 \ne -29 \\[3ex] $ The point (−7, −6) is not on the graph of the equation x = 4y − 5.
(d.) The statement is true.
For all real number domain:
To find the y-intercept:
set x to 0 and
solve for y
Hence: for $y = f(x)$,
$y = f(0)$ is the value of the y-intercept.
But, please note that y-intercept is a point.
So, the y-intercept = $(0, y-value)$