Course Announcements

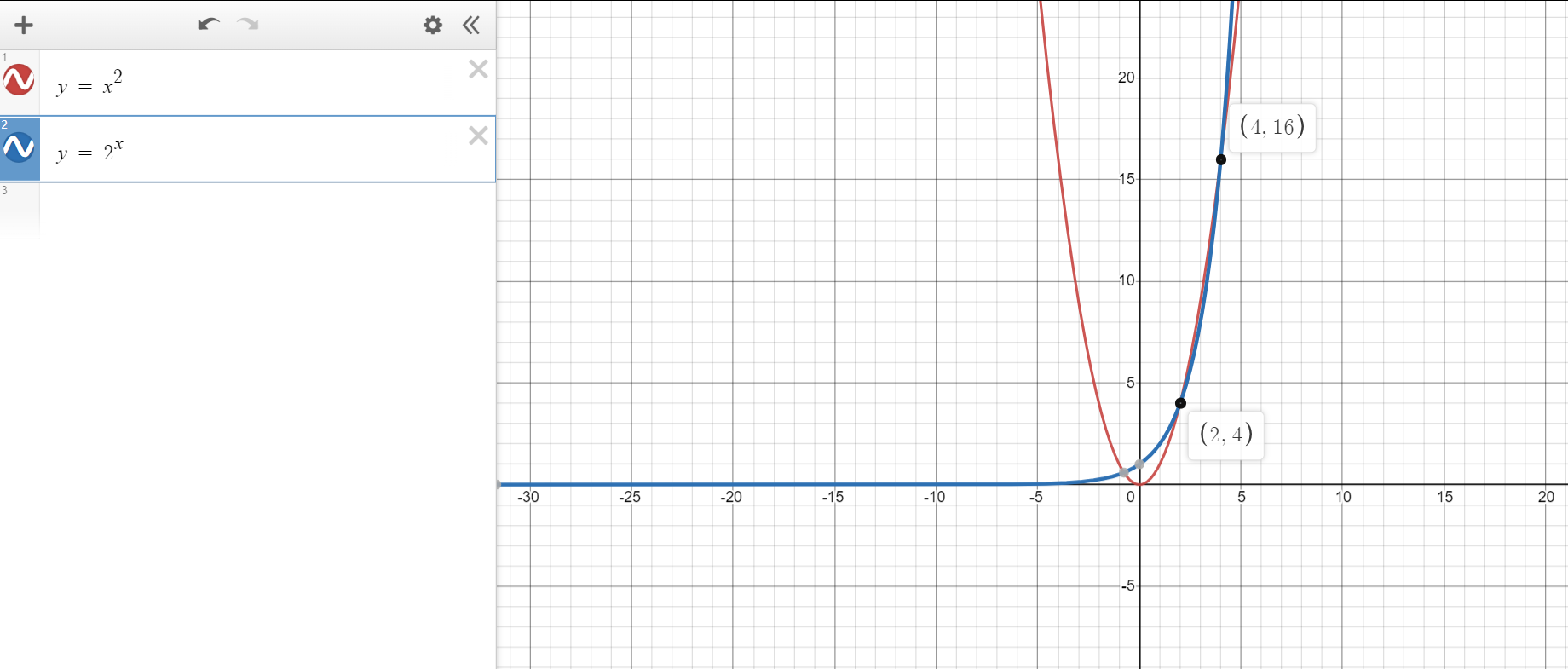
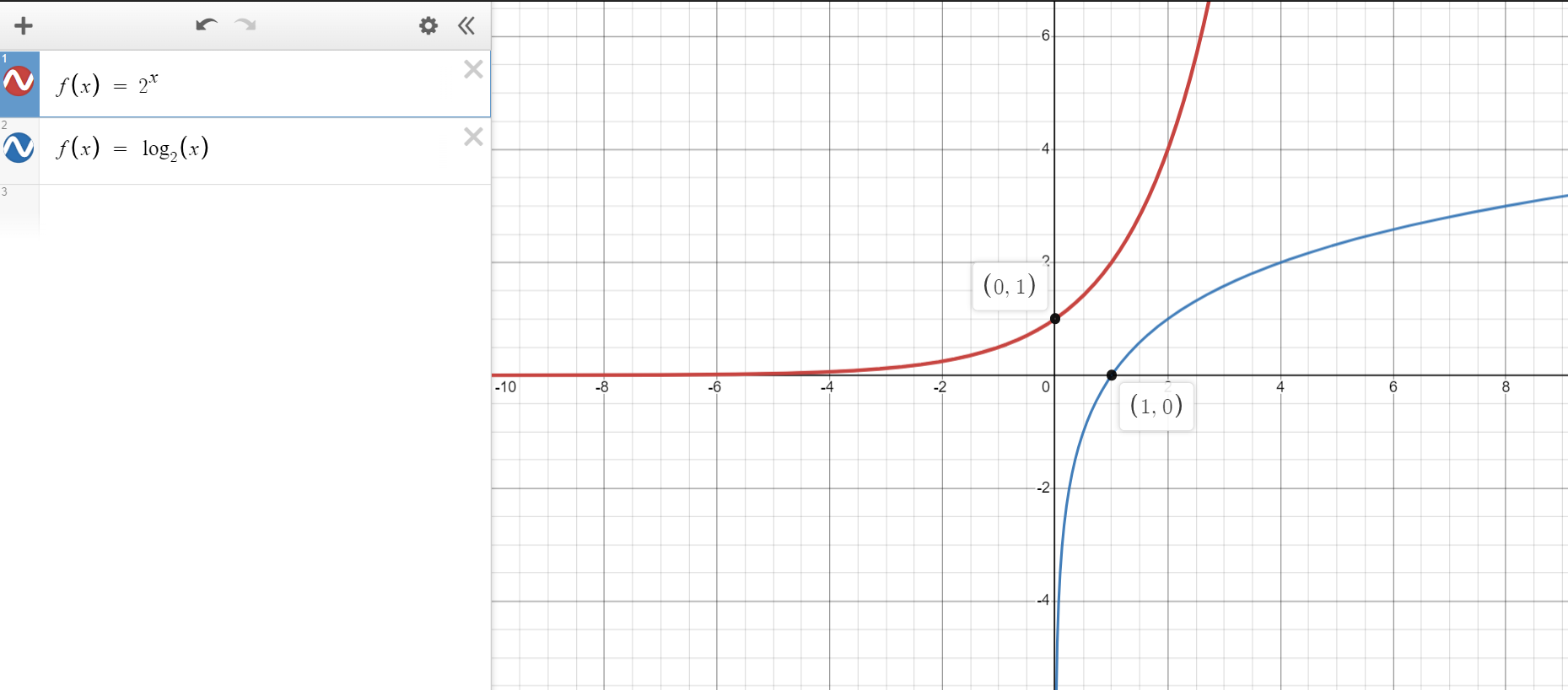
Welcome to Week 1: Relations and Functions

Great Students,

Greetings to everyone.
Welcome to Module 1.

Before I immigrated to the United States, I looked like this:


Then, I came here, ate a lot of cheeseburgers, gained a lot of weight, and now look like this:

(Please don't laugh at me) 😊

So we have two variables: weight and the number of cheeseburgers.
Which one depends on the other?
In other words:
(1.) Which of the variables is the dependent variable?
(2.) Which one is the independent variable?
(Hint: Does my weight depend on the number of cheeseburgers I eat, or does the number of cheeseburgers I eat depend on my weight?)

Questions for Thought: First Set
(1.) Did you notice any relationship?
What is the relationship?
Any input-output relationship?
Which variable is the input?
Which variable is the output?
(2.) Can you express that relationship as a Set of ordered pairs (set of points)?
(3.) Can you express that relationship as a Function Rule (Equation)?
(4.) Can you express that relationship as a Table of Values?
(5.) Can you express that relationship as a Graph?

This example is a two-variable relationship where the weight is the dependent variable and the number of cheeseburgers is the independent variable.
In the example, we say that the weight, w is a function of the number of cheeseburgers, c
We can write it as:
w = f(c)
Let us make some interdisciplinary connections:

Bring it to Algebra and Calculus
y is the dependent variable
x is the independent variable

Bring it to Statistics
y is the response variable
x is the predictor or explanatory variable

Bring it to Philosophy (Cause-Effect Relationship)
y is the effect
x is the cause

Bring it to Economics/Business (Input-Output Relationship)
y is the output
x is the input

Bring it to Psychology/Human Behavior/Sociology
y is the consequence
x is the action

So, for any input, there is at least an output. This is defined as a Relation.
Welcome to Relations.

Notice the word, at least in the definition of a Relation.
At least one output means one or more output.
But, is it possible for an input to have more than one output?
Is it possible for a BRCC student to have more than one Student ID?
Is it possible for an American to have more than one SSN?
Is it possible for a student to make more than one grade on the same test?

This leads us to these concepts:
Function
One-to-one Function (Injective Function)
Onto Function (Surjective Function)
Bijective Function

Questions for Thought: Second Set
Determine if these scenarios represent a relation, function, one-to-one function, onto function, surjective function.
Write all that is applicable.
(1.) A BRCC student has only one Student ID.
(2.) A BRCC student has more than one Student ID.
(3.) Two BRCC Students have the same grade on a Math quiz.
(4.) A BRCC student has two different grades on a Math quiz.
(5.) Every BRCC student was born by a woman.
Welcome to Functions.

May you please:
(1.) Click the Week 1 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 1 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success

Welcome to Week 2: Piecewise Functions; Transformations of Functions

Great Students,

Greetings to everyone.
Welcome to Module 2.

Last week, we discussed Relations and Functions.
We discussed the different types of functions and gave an example of each type.
This week, we shall continue our study on Functions. 
First: We shall review functions defined on a sequence of intervals (domains).
These are known as Piecewise Functions.
Second: We shall review a set of functions known as Toolbox Functions (also known as Parent Functions), where we transform these parent functions into child functions. 
(Relate it to Biology: Parents transform to give children.)

For this announcement, let us focus on Piecewise Functions.
May I introduce the topic by telling you a story? Yes, I tell stories too 😊

The event will hold in three days.
Well-cooked and delicious: rice and beans
Fresh avocados
Options of fish, chicken, cabeza
Son: Dad, what about vegan?
Dad: Let's not worry about vegan. Those folks would really be hungry.
They need to eat well.
Son: Does it mean that those who are vegan do not eat well?
Dad: I did not say that. Do not force words into my mouth.
Son: I just asked a question, Dad.
What about al pastor?
Dad: No, we do not eat pork.
Why should we give people what we do not eat?
Okay, let's go and order these burritos.

Dad: Buenas tardes, señora
How are you doing today?
Son: Good afternoon, Mama Esther.
Esther: Good afternoon. I am doing well.
How are you doing too?
Dad: We are doing well.
Thank you.
How much are your burritos?
Esther: It's $7.00 each.
Guacamole costs extra ¢50 each.
Dad: We want to place an order for 1000 burritos.
Son: Well-cooked: rice and beans; fresh avocados...everything
No guacamole.
Esther: Okay...
Dad: 300 pescado; 300 cabeza; 400 chicken
How much is the cost?
Esther: How soon do you need them?
Dad: In three days.
Esther: Would I deliver them, or would you pick them up?
Dad: We shall pick them up.
Esther: It's going to be $7 each for the first 300 burritos
$6 each for the next 300, and $5.00 each for the remaining 400.
Fair enough?
So, the price is ...
$2100 for the first 300 + $1800 for the next 300 + $2000 for the remaining 400
Total of $5900
Add 10% tax of $5900
That gives $590
Total cost of $6490.00

Son: Dad, I could calculate the cost another way.
Dad: What way?
Is it better than the way Esther did?
Son: For many orders, yes!
And for writing a computer program to calculate it.
Dad: Interesting. What is it?
Son: We learned it in school.
Mama Esther did it as a simple Arithmetic.
Mr. C called it the Manual method.
Then, he taught us to do it algebraically ...
using the Piecewise Function method.
I think it is much better.
Dad: Okay, what's the method?
Son: We begin by defining the variables involved.
Let the number of burritos = b
and the cost = c
Which variable depends on the other variable?
Son: Does the number of burritos depend on the cost, or
does the cost depend on the number of burritos?
Dad: The cost depends on the number of burritos.
Son: That is correct.
We write it this way: $c = f(b)$
It can also be written as: $c(b)$
Dad: Okay...
Son: So,

$ c(b) = \begin{cases} 7b; & \quad 1 \leq b \leq 300 \\[3ex] 6b + 300; & \quad 300 \lt b \leq 600 \\[3ex] 5b + 900; & \quad 600 \lt b \leq 1000 \end{cases} $

Dad: How is this better than the way Esther did it?
Son: Say you wanted to order $900$ burritos
How much would it cost excluding the taxes?
Dad: $7 for the first 300 gives $2100
$6 for the next 300 gives $1800
$5 for the remaining 300 gives $1500
That gives a total of $5400
Son: How many steps did you do before you got the answer?
Dad: Three steps...
Son: I shall do only two steps before I get that answer.
$c(900) = 5(900) + 900 = 4500 + 900 = 5400$
Dad: You used the 3rd equation because 900 falls in ...
Son: that piece...yes...in that domain.
Dad: That is interesting! How did you get those equations?
Son: Welcome to Piecewise Functions!, Dad.

Welcome to Piecewise Functions.

May you please:
(1.) Click the Week 2 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 2 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success

Welcome to Week 3: Linear Functions and Linear Models

Great Students,

Greetings to everyone.
Welcome to Module 3.

Last week, we discussed Piecewise Functions and the Transformation of Functions.
This week, we shall continue our study on Functions.
First: We shall discuss Linear Functions.
Second: We shall discuss Linear Models.

Recall the example we discussed in Week 1 regarding weight, w and the number of cheeseburgers, c
Say we express the relation as a table.

Based on the table:
When I ate a cheeseburger, I gained 3 pounds.
When I ate two cheeseburgers, I gained 6 pounds.
When I ate three cheeseburgers, I gained 9 pounds.
When I ate four cheeseburgers, I gained 12 pounds.

Questions for Thought:
(1.) (a.) What is the relationship?
(b.) What kind of relationship is it?
(c.) Which variable is the input?
(d.) Which variable is the output?

(2.) Can you express that relationship as a set of ordered pairs (set of points)?
(3.) Can you express that relationship as a function rule (equation)?
(4.) Can you express that relationship as a graph?
(5.) For every 1 cheeseburger I ate (unit increase in the input), how does that affect my weight (the output)?

(6.) (a.) What concept was asked in Question (5.)?
(b.) Is that a positive, negative, or zero?

(7.) Can you give examples/scenarios of a negative slope?
(Hint: the output decreases for every unit increase in the input)

(8.) Can you give examples/scenarios of a zero slope?
(Hint: the output remains the same for every unit increase in the input.)

Welcome to Linear Functions.

May you please:
(1.) Click the Week 3 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 3 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success

Welcome to Week 4: Quadratic Functions, Quadratic Models, and Quadratic Inequalities

Great Students,

Greetings to everyone.
Welcome to Module 4.

Last week, we discussed Linear Functions and Linear Models.
This week, we shall continue our study on Functions and then extend our study to Inequalities.
First: We shall discuss Quadratic Functions.
Second: We shall discuss Quadratic Models.
Third: We shall discuss Quadratic Inequalities.

Let us focus on Quadratic Functions by discussing an important application.
What are the two main goals of every business?...yes...even for non-profit organization?
(1.) Maximize Profit.
(2.) Minimize Cost/Loss.
(Did you notice the words in bold? By the way, you can add those words in your resume and put it in the context of your discipline).

If we can model a business, say a business that sells laptops; we can determine the number of laptops that should be sold during a specific period to generate the maximum revenue and hence, the maximum profit.
We can also determine the maximum revenue and the maximum profit.

If we can model a business, say a business that produces citrus trees during the winter season; we can determine the amount of fertilizers to order each month during the winter season to minimize the total cost of producing the citrus trees. 

Welcome to Quadratic Functions.

May you please:
(1.) Click the Week 4 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 4 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success

Welcome to Week 5: Polynomials

Great Students,

Greetings to everyone.
Welcome to Module 5.

For the past four weeks, we have been discussing Functions.
This week, we shall look at a special type of function: Polynomials. 
Mathematicians wanted to study the properties of functions with only nonnegative integer exponents: constants, linear functions, quadratic functions, cubic functions and quartic functions among others.
(Notice the term: nonnegative. What is the difference between a positive integer and a non-negative integer?)
These types of functions are special. We call them: Polynomials.
A polynomial is first and foremost a function.
Then, a polynomial is that special type of function because it has only non-negative integer exponents.
We shall discuss polynomials, perform arithmetic operations on polynomials, and factor polynomials.

Factoring a Polynomial is the breaking/splitting of the polynomial into a product of factors such that the product of those factors gives the polynomial.
This implies that if the product of the factors do not give us the polynomial, there is a high probability that the factoring was not done well. So, it is always important to check your solution by multiplying the product of the factors.
Multiplying polynomials gives the product of two or more polynomials. 
Factoring that product gives the product of the two or more polynomials.
(Compare: Multiplying and Factoring to Computer Assembly and Computer Disassembly)
We use factoring techniques to factor polynomials. 

Welcome to Polynomials.

May you please:
(1.) Click the Week 5 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 5 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success

Welcome to Week 6: Rational Functions

Great Students,

Greetings to everyone.
Welcome to Module 6.

Last week, we discussed the topic of Polynomials.
This week, we shall discuss the ratio (or quotient) of two polynomials.
Before we continue, do you recall these terms in Arithmetic:
Rational Number
Irrational Number

Ratio involves a fraction.
A fraction implies that there is a numerator and a denominator.
Having a denominator means that there should be a condition: there should not be division by zero. Can you divide something by nothing?
So, let us reword what we shall this week: ratio of two polynomials where the denominator is not zero. That condition regarding the denominator is important.
So, we say that: a rational function is the ratio of two polynomials where the denominator is not zero.
Just as we observed that polynomials have some properties, we shall also observe that rational functions have some properties.
We shall discuss these properties of rational functions, graph rational functions, and solve applied problems on rational functions among others.

Welcome to Rational Functions.

May you please:
(1.) Click the Week 6 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 6 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success

Welcome to Week 7: Polynomial Inequalities; Rational Inequalities; and Polynomial Theorems

Great Students,

Greetings to everyone.
Welcome to Module 7.

Last two weeks, we discussed the topic of Polynomials.
Last week, we discussed the topic of Rational Functions. As stated then, a rational function is a quotient of two polynomials where the denominator is not zero.
Most of the problems we solved dealt with the functions as expressions and the functions as equations (equalities).
But what about solving the functions as inequalities? Well, that is what we shall study this week. 
This week, we shall continue our study on Polynomials and Rational Functions but we shall be discussing the functions as inequalities. We shall also discuss several theorems on polynomial functions. 

Specifically, we shall discuss: 
Polynomial Inequalities
Rational Inequalities
Polynomial Theorems

Welcome to Polynomial Inequalities; Rational Inequalities; and Polynomial Theorems.

May you please:
(1.) Click the Week 7 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 7 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success

Welcome to Week 8: Composite Functions and Inverse Functions

Great Students,

Greetings to everyone.
Welcome to Module 8.

Last week, we discussed Polynomial Inequalities and Rational Inequalities.
This week, we shall discuss the Composition of Functions and the Inverse of Functions.
For this announcement, let us focus on the Composition of Functions.

Say you visit your favorite retail store
You want to buy a bag
Say the cost of each bag = $20.00
You want to buy 10 bags
10 bags @ $20.00 per bag = $10 * 20$ = $200.00
Say the sales tax = 10%
10% sales tax = $\dfrac{10}{100} * 200$ = $$20.00$
Total Cost = $200.00 + 20.00$ = $$220.00$
Notice how we wrote all these steps just to calculate the total cost of a single item?

Is there another way (preferably an easier way) to calculate the total cost?
May we just write functions to make it easier for us to do?

Let:
x = number of bags
Cost function = $C(x)$
This means that:
$C(x) = 20x$
This is one function.
Let us form another function.

Let:
d = dollar
Total cost function = $T(d)$
$T(d) = d + 10\%d$
But, the cost is a function of x
The total cost is also a function of x
Yes, it is a function of the dollar; but the dollar is also a function of the number of bags, x

$ T(d) = d + 0.1d \\[3ex] T(d) = 1.1d \\[3ex] $ Let us now find the composition of $T$ and $C$
This will be written as:
$T(C(x))$
But why???
Before we find the cost function, we have to find the total cost function.
We work from inside to outside
We strive to be good inwards before we are good outwards
Do you remember the saying: Charity begins at home?
Here is the thing: We want one function that will just calculate the total cost.
What is one function of one variable (one independent variable) that will give the total cost without having to go through all those initial steps?

$ So: \\[3ex] T(d) = 1.1 d \\[3ex] \therefore T(C(x)) = 1.1 * C(x) \\[3ex] T(C(x)) = 1.1 * 20x \\[3ex] T(C(x)) = 22x \\[3ex] $ This is what we need.
So, for $x = 10$ bags, $T(C(20)) = 22 * 10$ = $220.00

Does this make sense?
Do you see the importance of the composition of functions?

With the composition of functions, we can get two or more different functions of the same variable, and compose them into just one function of that variable.
Say we have two functions of a variable, $x$;
$f(x)$ and $g(x)$
$f(x)$ is read as $f \:of\: x$
$g(x)$ is read as $g \:of\: x$
Then;
$f$ composed with $g$ of $x$ = $(f \circ g)(x)$
Alternatively, we can say:
The composition of $f$ and $g$ of $x$ = $(f \circ g)(x)$
Similarly;
$(g \circ f)(x)$ is the composition of $g$ and $f$ of $x$
OR
$(g \circ f)(x)$ is $g$ composed with $f$ of $x$

$ (f \circ g)(x) = f(g(x)) \\[3ex] (g \circ f)(x) = g(f(x)) \\[3ex] $ Do the inner function first.
Do the outer function of the result of the inner function next.

For $f(g(x))$:
Do $g(x)$ first
Then, do $f(...what \:you\: have)$ next

For $g(f(x))$:
Do $f(x)$ first
Then, do $g(...what \:you\: have)$ next

Can we have more than two functions composed as a single function?

Say we have three functions of x:
x = independent variable

$ f(x) \\[3ex] g(x) \\[3ex] h(x) \\[3ex] $ $f(g(h(x)))$ means that we do:
$h(x)$ first
then, do $g(...what \:you\: have)$ next
then, do $f(...what \:you\: have)$ next

Do you notice any relationship between Evaluating Functions, Operations on Functions, and the Composition of Functions?
Do you see why we learn one topic before the other?

The result of two or more functions composed as a single function is a Composite Function.
We use the Composition of Functions to Test for Inverses of Functions.
Welcome to Composite Functions and Inverse Functions.

May you please:
(1.) Click the Week 8 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 8 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success

Welcome to Week 9: Exponential Functions and Logarithmic Functions

Great Students,

Greetings to everyone.
Welcome to Module 9.

Last week, one of the topics we discussed was Inverse Functions.
This week, we shall review two functions that are inverses of each other. These two functions have various applications in many fields of life including the Medical and Health Sciences, the Engineering fields and Business/Finance disciplines among others.
They are Exponents and Logarithms which leads to Exponential Functions and Logarithmic Functions.

Let us begin a story. You already know I tell stories. 😊

Virologist: It is a virus.
It is highly contagious.
It is spreading so fast.

Mathematician: GOD help us!
How fast is it spreading?

Statistician: On the first day (Day 1), two people contacted it.
On the second day (Day 2), four people contacted it.
On the third day (Day 3), nine people contacted it.
On the fourth day (Day 4), sixteen people were affected.
On the fifth day (Day 5), twenty five people were affected.
On the sixth day (Day 6), thirty six people were affected.
On the seventh day, (Day 7), forty nine people tested positive for the virus.

Teacher: If this trend continues, how many people are likely to be infected on the ninth day?
What type of function does this scenario represent?
What is the graph of that function called?

Can we represent this information in a table?

Social Worker: Wait a minute!
We have an updated report.
Here it is:

On the first day (Day 1), two people contacted it.
On the second day (Day 2), four people contacted it.
On the third day (Day 3), eight people contacted it.
On the fourth day (Day 4), sixteen people were affected.
On the fifth day (Day 5), thirty two people were affected.
On the sixth day (Day 6), sixty four people were affected.
On the seventh day, (Day 7), one hundred and twenty eight people tested positive for the virus.

Teacher: If this trend continues, how many people are likely to be infected on the ninth day?
What type of function does this scenario represent?

Can we represent this updated information in a table?

Teacher: Do you see the difference between a Quadratic Function and an Exponential Function?
Do you see the difference between $x^2$ and $2^x$?

Let us see a visual explanation of these functions


Ask students to compare and contrast the two functions based on their graphs.
Note their responses.
Ask them to mention some life scenarios of Exponential Growth: increasing at a fast rate and Exponential Decay: decreasing at a fast rate"?

Our focus is on Exponential Functions and Logarithmic Functions
Let us attempt another question based on this story.

Teacher: If this trend continues, on what day will about four thousand and ninety six people be infected?
What type of function does this scenario represent?

Let us represent all these information on a table so we can see the relationship between Exponents and Logarithms.

Practice! Practice!! Practice!!!
Given: an exponential function
Write: the logarithmic function

Similary
Given: a logarithmic function
Write: the exponential function

Let us see a visual explanation of these functions


$ Exponential\;\;Function:\;\;y = 2^x \\[3ex] Logarithmic\;\;Function:\;\;y = \log_2{x} \\[5ex] Exponential\;\;Function:\;\;(0, 1) \\[3ex] 2^0 = 1 \\[3ex] Logarithmic\;\;Function:\;\; (1, 0) \\[3ex] \log_{2}{1} = 0 \\[5ex] Exponential\;\;Function:\;\;(1, 2) \\[3ex] 2^1 = 2 \\[3ex] Logarithmic\;\;Function:\;\; (2, 1) \\[3ex] \log_{2}{2} = 1 \\[5ex] Exponential\;\;Function:\;\;(2, 4) \\[3ex] 2^2 = 4 \\[3ex] Logarithmic\;\;Function:\;\; (4, 2) \\[3ex] \log_{2}{4} = 2 \\[5ex] $ Review: Composition of Functions and Inverse Functions.
Ask students to compare and contrast the two functions based on their graphs.
Note their responses.
Ask students to verify that both functions are inverses of each other.
In other words, Test for Inverses

Welcome to Exponential Functions and Logarithmic Functions.

May you please:
(1.) Click the Week 9 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 9 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success

Welcome to Week 10: Exponential Equations; Logarithmic Equations; Linear Systems; and Matrices

Great Students,

Greetings to everyone.
Welcome to Module 10.

Last week, we discussed the topics of Exponential Functions and Logarithmic Functions.
This week, we shall continue our study on Exponents and Logarithms by solving exponential equations and logarithmic equations.
Then, we shall discuss linear systems and matrices. Specifically, we shall use the Gauss-Jordan method (also known as the Gaussian Elimination method) to solve matrices and linear systems.
As you probably know, one of the applications of linear systems is Mixology.
Let us look at this example.

Timothy likes to drink.
However, he does not like strong drinks.
During his birthday party, he received several alcoholic drinks as gifts.
One of the gifts was a vodka containing 40% alcohol by volume (40% ABV).
He wants a 5-liter solution containing 16% alcohol. So, he mixes the wine with the vodka.
How many liters of each drink (wine and vodka) should he mix?

Solution:
Let the volume of the 10% alcohol wine be x
Let the volume of the 40% alcohol vodka be y
Volume of the mixture = x + y

Volume: x + y = 5 ...eqn.(1)

Concentration: 10% of x + 40% of y = 16% of the mixture
0.1x + 0.4y = 0.16(5)
0.1x + 0.4y = 0.8 ...eqn.(2)
x + 4y = 8 ...modified eqn.(2)

So, the two equations are:

$ x + y = 5 ...eqn.(1) \\[3ex] x + 4y = 8 ...eqn.(2) \\[5ex] \underline{Elimination-by-Subtraction\;\;Method} \\[3ex] To\;\;find\;\;y,\;\;eliminate\;\;x \\[3ex] eqn.(2) - eqn.(1) \implies \\[3ex] (x + 4y) - (x + y) = 8 - 5 \\[3ex] x + 4y - x - y = 3 \\[3ex] 3y = 3 \\[3ex] y = \dfrac{3}{3} \\[5ex] y = 1 \\[3ex] y = 1\;liter \\[5ex] \underline{Elimination-by-Addition\;\;Method} \\[3ex] To\;\;find\;\;x,\;\;eliminate\;\;y \\[3ex] -4 * eqn.(1) + eqn.(2) \implies \\[3ex] -4(x + y) + (x + 4y) = -4(5) + 8 \\[3ex] -4x - 4y + x + 4y = -20 + 8 \\[3ex] -3x = -12 \\[3ex] x = \dfrac{-12}{-3} \\[5ex] x = 4 \\[3ex] x = 4\;liters \\[3ex] $ Interpretation/Conclusion/Decision:
Timothy should mix 4 liters of the 10% alcohol wine with 1 liter of the 40% alcohol vodka to obtain 5 liters of the 16% alcohol solution.

Welcome to Exponential Equations; Logarithmic Equations; Linear Systems; and Matrices.

May you please:
(1.) Click the Week 10 module.
(2.) Review the Overview and Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 10 Discussion.
(6.) Attend the Live Sessions/Student Engagement Hours for this week.

Should you have any questions, please ask. I am here to help.
Thank you.

Samuel Chukwuemeka
Working together for success