For ACT Students The ACT is a timed exam...60 questions for 60 minutes
This implies that you have to solve each question in one minute.
Some questions will typically take less than a minute a solve.
Some questions will typically take more than a minute to solve.
The goal is to maximize your time. You use the time saved on those questions you solved in less than a minute, to solve the questions that will take more than a minute.
So, you should try to solve each question correctly and timely.
So, it is not just solving a question correctly, but solving it correctly on time.
Please ensure you attempt all ACT questions.
There is no negative penalty for a wrong answer.
For JAMB and NZQA Students
Calculators are not allowed. So, the questions are solved in a way that does not require a calculator.
For NSC Students
For the Questions:
Any space included in a number indicates a comma used to separate digits...separating multiples of three digits from behind.
Any comma included in a number indicates a decimal point.
For the Solutions:
Decimals are used appropriately rather than commas
Commas are used to separate digits appropriately.
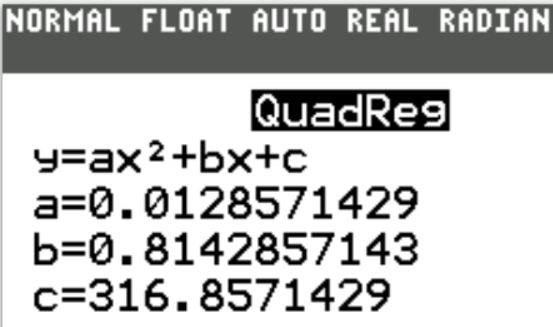
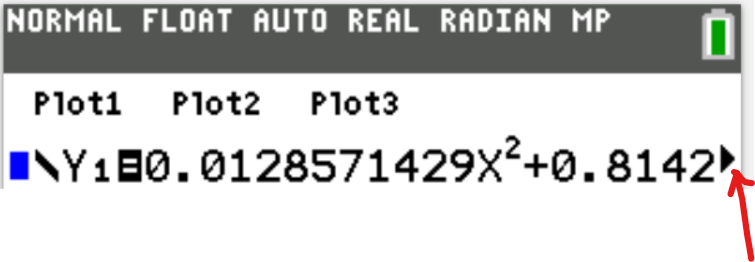
The Forms of a Quadratic Function are:
(1.) Standard Form/General Form
Note that the standard form is written in descending order of x
$ y = ax^2 + bx + c \\[3ex] OR \\[3ex] f(x) = ax^2 + bx + c \\[3ex] Vertex = \left[-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right] \\[5ex] $ (2.) Vertex Form
$ y = a(x - h)^2 + k \\[3ex] OR \\[3ex] f(x) = a(x - h)^2 + k \\[3ex] Vertex = (h, k) \\[3ex] h = x-coordinate\;\;of\;\;the\;\;vertex \\[3ex] k = y-coordinate\;\;of\;\;the\;\;vertex \\[3ex] $ (3.) Extended Vertex Form
$ f(x) = a(x - h)^2 + k ...Vertex\;\;Form \\[3ex] f(x) = a\left(x + \dfrac{b}{2a}\right)^2 + \dfrac{4ac - b^2}{4a}...Extended\;\;Vertex\;\;Form \\[5ex] Vertex = (h, k) \\[3ex] \implies \\[3ex] -h = \dfrac{b}{2a} \\[5ex] h = -\dfrac{b}{2a} \\[5ex] k = \dfrac{4ac - b^2}{4a} \\[5ex] \implies \\[3ex] \boldsymbol{Vertex = (h, k) = \left(-\dfrac{b}{2a}, \dfrac{4ac - b^2}{4a}\right)} \\[5ex] $ Attempt all questions.
Show all work.
(1.) The price p (in dollars) and the quantity x sold of a certain product satisfy the demand equation x = −9p + 900
(a.) Find a model that expresses the revenue R as a function of p.
(Remember R = xp.)
(b.) What is the domain of R?
Assume R is nonnegative.
(c.) What price p maximizes revenue?
Simplify your answer. Type an integer or decimal.
(d.) What is the maximum revenue?
Simplify your answer. Type an integer or decimal.
(e.) How many units are sold at this price?
Simplify your answer. Type an integer or decimal.
(f.) Graph R
(g.) What price should the company charge to earn at least $10,179 in revenue?
Simplify your answer. Type an integer or decimal.
$ (a.) \\[3ex] R(p) = x * p \\[3ex] = p * x \\[3ex] = p(-9p + 900) \\[3ex] = -9p^2 + 900p \\[3ex] $ (b.) The revenue cannot be negative.
The revenue can be zero (no revenue)
The revenue can be positive
Hence, the revenue must be nonnegative
The domain of R includes all the real number prices such that the revenue is nonnegative
$ R(p) \ge 0 \\[3ex] -9p^2 + 900p \ge 0 \\[3ex] -9(p^2 - 100p) \ge 0 \\[3ex] p^2 - 100p \le \dfrac{0}{-9} \\[5ex] p^2 - 100p \le 0 \\[3ex] p(p - 100) \le 0 \\[3ex] Assume:\;\;p(p - 100) = 0 \\[3ex] p = 0 \;\;\;OR\;\;\; p - 100 = 0 \\[3ex] p = 0 \;\;\;OR\;\;\; p = 100 \\[3ex] Test\;\;Intervals\;\;are: \\[3ex] p \lt 0 \\[3ex] 0 \le p \le 100 \\[3ex] p \gt 100 \\[3ex] $
Less than or equal to zero means nonnegative
Hence, the second test interval gives the solution of the inequality
Domain, D = {p | 0 ≤ p ≤ 100}
(c.) The price that maximizes revenue is the x-coordinate of the vertex of the revenue function.
$ R(p) = -9p^2 + 900p \\[3ex] Compare:\;\;R(p) = ap^2 + bp + c \\[3ex] a = -9 \\[3ex] b = 900 \\[3ex] x-coordinate\;\;of\;\;vertex = -\dfrac{b}{2a} \\[5ex] p = \dfrac{-900}{2(-9)} \\[5ex] = \dfrac{-900}{-18} \\[5ex] = 50 \\[3ex] $ The price that maximizes revenue is $50
(d.) The maximum revenue is the y-coordinate of the vertex of the revenue function.
$ R(p) = -9p^2 + 900p \\[3ex] p = \$50 \\[3ex] y-coordinate\;\;of\;\;vertex = R(50) \\[3ex] R(50) = -9(50)^2 + 900(50) \\[3ex] = -9(2500) + 45000 \\[3ex] = -22500 + 45000 \\[3ex] = 22500 \\[3ex] $ The maximum revenue is $22,500
(e.) The number of units sold at this price is the value of x for which R = $22500
$ vertex = (x, y) = (p, R) = (50, 22500) \\[3ex] R = xp \\[3ex] xp = R \\[3ex] x = \dfrac{R}{p} \\[5ex] x = \dfrac{22500}{50} \\[5ex] x = 450 \\[3ex] $ 450 units were sold at the price that gave the maximum revenue.
(f.) The graph of the revenue versus price is shown below.
Keep in mind that the vertex is (p, R) = (50, 22500)
Options (A.) and (D.) are similar.
However, option (A.) is the graph of R versus p while option (D.) is the graph of p versus R
The revenue, R is the y-axis
The price that maximizes the revenue, p is the x-axis
So, the correct graph should be the graph of R versus p: option (A.)
(g.) The price that the company should charge to earn at least $10,179
At least 10179 means ≥ 10179
They are asking us to determine the price range for which the revenue is greater than or equal to $10,179
$ -9p^2 + 900p \ge 10179 \\[3ex] -9p^2 + 900p - 10179 \ge 0 \\[3ex] -9(p^2 - 100p + 1131) \ge 0 \\[3ex] p^2 - 100p + 1131 \le \dfrac{0}{-9} \\[5ex] p^2 - 100p + 1131 \le 0 \\[3ex] (p - 13)(p - 87) \le 0 \\[3ex] Assume:\;\;(p - 13)(p - 87) = 0 \\[3ex] p - 13 = 0 \;\;\;OR\;\;\; p - 87 = 0 \\[3ex] p = 13 \;\;\;OR\;\;\; p = 87 \\[3ex] Test\;\;Intervals\;\;are: \\[3ex] p \lt 13 \\[3ex] 13 \le p \le 87 \\[3ex] p \gt 87 \\[3ex] $
Less than or equal to zero means nonnegative
Hence, the second test interval gives the solution of the inequality
The solution is: {p | 13 ≤ p ≤ 87}
The company should a price between a minimum of $13.00 and a maximum of $87.00
(a.) Find a model that expresses the revenue R as a function of p.
(Remember R = xp.)
(b.) What is the domain of R?
Assume R is nonnegative.
(c.) What price p maximizes revenue?
Simplify your answer. Type an integer or decimal.
(d.) What is the maximum revenue?
Simplify your answer. Type an integer or decimal.
(e.) How many units are sold at this price?
Simplify your answer. Type an integer or decimal.
(f.) Graph R
(g.) What price should the company charge to earn at least $10,179 in revenue?
Simplify your answer. Type an integer or decimal.
$ (a.) \\[3ex] R(p) = x * p \\[3ex] = p * x \\[3ex] = p(-9p + 900) \\[3ex] = -9p^2 + 900p \\[3ex] $ (b.) The revenue cannot be negative.
The revenue can be zero (no revenue)
The revenue can be positive
Hence, the revenue must be nonnegative
The domain of R includes all the real number prices such that the revenue is nonnegative
$ R(p) \ge 0 \\[3ex] -9p^2 + 900p \ge 0 \\[3ex] -9(p^2 - 100p) \ge 0 \\[3ex] p^2 - 100p \le \dfrac{0}{-9} \\[5ex] p^2 - 100p \le 0 \\[3ex] p(p - 100) \le 0 \\[3ex] Assume:\;\;p(p - 100) = 0 \\[3ex] p = 0 \;\;\;OR\;\;\; p - 100 = 0 \\[3ex] p = 0 \;\;\;OR\;\;\; p = 100 \\[3ex] Test\;\;Intervals\;\;are: \\[3ex] p \lt 0 \\[3ex] 0 \le p \le 100 \\[3ex] p \gt 100 \\[3ex] $
|
Let: |
p < 0 p = −1 |
0 ≤ p ≤ 100 p = 1 |
p > 100 p = 101 |
|---|---|---|---|
| $p$ | − | + | + |
| $p - 100$ | − | − | + |
| $p(p - 100)$ | + | − | + |
Less than or equal to zero means nonnegative
Hence, the second test interval gives the solution of the inequality
Domain, D = {p | 0 ≤ p ≤ 100}
(c.) The price that maximizes revenue is the x-coordinate of the vertex of the revenue function.
$ R(p) = -9p^2 + 900p \\[3ex] Compare:\;\;R(p) = ap^2 + bp + c \\[3ex] a = -9 \\[3ex] b = 900 \\[3ex] x-coordinate\;\;of\;\;vertex = -\dfrac{b}{2a} \\[5ex] p = \dfrac{-900}{2(-9)} \\[5ex] = \dfrac{-900}{-18} \\[5ex] = 50 \\[3ex] $ The price that maximizes revenue is $50
(d.) The maximum revenue is the y-coordinate of the vertex of the revenue function.
$ R(p) = -9p^2 + 900p \\[3ex] p = \$50 \\[3ex] y-coordinate\;\;of\;\;vertex = R(50) \\[3ex] R(50) = -9(50)^2 + 900(50) \\[3ex] = -9(2500) + 45000 \\[3ex] = -22500 + 45000 \\[3ex] = 22500 \\[3ex] $ The maximum revenue is $22,500
(e.) The number of units sold at this price is the value of x for which R = $22500
$ vertex = (x, y) = (p, R) = (50, 22500) \\[3ex] R = xp \\[3ex] xp = R \\[3ex] x = \dfrac{R}{p} \\[5ex] x = \dfrac{22500}{50} \\[5ex] x = 450 \\[3ex] $ 450 units were sold at the price that gave the maximum revenue.
(f.) The graph of the revenue versus price is shown below.
Keep in mind that the vertex is (p, R) = (50, 22500)
Options (A.) and (D.) are similar.
However, option (A.) is the graph of R versus p while option (D.) is the graph of p versus R
The revenue, R is the y-axis
The price that maximizes the revenue, p is the x-axis
So, the correct graph should be the graph of R versus p: option (A.)
(g.) The price that the company should charge to earn at least $10,179
At least 10179 means ≥ 10179
They are asking us to determine the price range for which the revenue is greater than or equal to $10,179
$ -9p^2 + 900p \ge 10179 \\[3ex] -9p^2 + 900p - 10179 \ge 0 \\[3ex] -9(p^2 - 100p + 1131) \ge 0 \\[3ex] p^2 - 100p + 1131 \le \dfrac{0}{-9} \\[5ex] p^2 - 100p + 1131 \le 0 \\[3ex] (p - 13)(p - 87) \le 0 \\[3ex] Assume:\;\;(p - 13)(p - 87) = 0 \\[3ex] p - 13 = 0 \;\;\;OR\;\;\; p - 87 = 0 \\[3ex] p = 13 \;\;\;OR\;\;\; p = 87 \\[3ex] Test\;\;Intervals\;\;are: \\[3ex] p \lt 13 \\[3ex] 13 \le p \le 87 \\[3ex] p \gt 87 \\[3ex] $
|
Let: |
p < 13 p = 0 |
13 ≤ p ≤ 87 p = 17 |
p > 87 p = 87 |
|---|---|---|---|
| $p - 13$ | − | + | + |
| $p - 87$ | − | − | + |
| $(p - 13)(p - 87)$ | + | − | + |
Less than or equal to zero means nonnegative
Hence, the second test interval gives the solution of the inequality
The solution is: {p | 13 ≤ p ≤ 87}
The company should a price between a minimum of $13.00 and a maximum of $87.00
